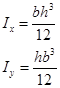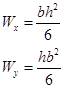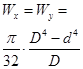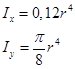Annet arealmoment

Annet arealmoment  er en geometrisk størrelse som er definert som følger:

                  

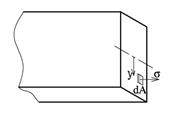
Annet arealmoment refererer alltid til en akse. I_y betyr f.eks. ”annet arealmoment om y-aksen”, og her inngår z² hvor z er avstanden normalt til y-aksen. For å bestemme annet arealmoment må vi integrere over en flate, typisk et bjelketverrsnitt. I og med at avstanden som inngår kvadreres behøver vi ikke ta hensyn til fortegn. Annet arealmoment kan beregnes om enhver akse (men aksen må ligge i samme plan som flaten), så lenge avstanden som inngår i integrasjonsuttrykket står vinkelrett på aksen. Annet arealmoment er sterkt avhengig av aksen som momentet regnes om, og vi må derfor angi referanseaksens orientering og beliggenhet.

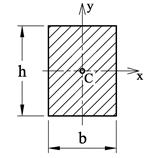
I bøyespenningsformelen skal annet arealmoment beregnes for bjelketverrsnittet om den aksen som bjelken bøyes om, og denne aksen skal gå gjennom tverrsnittets arealsenter (vi bruker y_o og z_o om disse aksene). Figuren viser de to viktigste aksene for en typisk bjelkeprofil. I_yo brukes for bjelker som bøyes om profilets sterke akse mens I_zo brukes ved bøyning om profilets svake akse.

Annet arealmoment er en viktig geometrisk størrelse i mekanikk og den er kjent under forskjellige navn, f.eks. arealtreghetsmoment. Annet arealmoment er kun et matematisk hjelpemiddel, og uttrykket har ingen fysisk betydning. Annet arealmoment kan hentes fra profiltabeller eller beregnes og vi skal se nærmere på dette litt senere.

Motstandsmoment

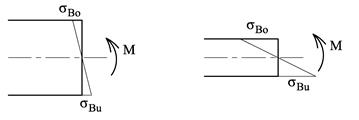
Bøyespenningsformelen gir oss s_B for ethvert punkt på snittet. I dimensjoneringsoppgaver er vi først og fremst interessert i å bestemme de største bøyespenningene dvs. s_Bu og s_Bo, og det er derfor vanlig å forenkle bøyespenningsformelen på følgende vis:

Tilsvarende kan vi sette opp

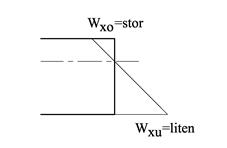
W_xo og W_xu kalles tverrsnittets motstandsmomenter om x-aksen og er rent geometriske størrelser. For symmetriske tverrsnitt er y_o = y_u og dermed blir W_x = W_xo = W_xu. Fra flattstål-eksemplet ser vi at en rektangulær flate har:

 og

For ikke-symmetriske profiler er vi mest interessert i den minste av W_xo og W_xu dvs. den som gir oss spenningene lengst vekk fra nøytralaksen (jo mindre motstandsmoment desto større spenninger) og i profiltabeller finner vi derfor bare W_x som den minste av W_xo og W_xu.

Både annet arealmoment og motstandsmomentet er geometriske uttrykk for profilets motstand i forhold til bøyning, dvs. jo større annet arealmoment og motstandsmoment, desto mindre blir spenningene ved et gitt bøyemoment.

Legg merke til at de største spenningene er omvendt proporsjonale med b og h², og det betyr at profilets høyde har en svært gunstig innvirkning på bøyespenningene. En dobling av profilhøyden reduserer bøyespenningene til en fjerdedel, og reduksjonen skyldes delvis økt areal og delvis større momentarm som reduserer kraften i kraftparet. 

 

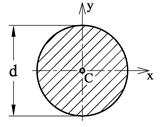
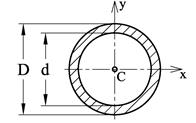
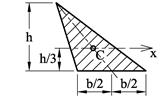
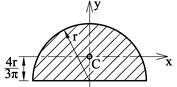
Tabellen under viser et utdrag fra formelsamlingen hvor vi finner uttrykk for I og W for enkle tverrsnitt. Vi kan også finne I og W for standardprofiler i tabeller fra stålleverandører, standarder el.l. For mer spesielle tverrsnitt er vi nødt til selv å beregne I og W og vi skal senere se hvordan dette gjøres.

Flategeometri

Snittflate	Annet arealmoment	Motstandsmoment	Polart arealmoment