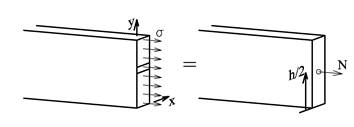
Figuren viser en flattstål-bjelke hvor det virker jevnt fordelte normalspenninger σ_A over tverrsnittet. Normalspenningene skyldes at det går en normalkraft N gjennom bjelken. Vi husker at N egentlig er resultanten til normalspenningene, og vi ønsker å bestemme beliggenheten til denne spenningsresultanten. Vi bruker x-aksen som referanse, se figur. Momentet for en liten delflate blir dM = y·σdA. Vi summerer opp momentene over hele tverrsnittet og bestemmer normalkraftens beliggenhet vha. momentteoremet:

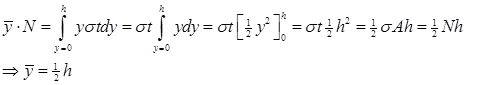
Resultantens beliggenhet i forhold til y-asken blir . For flattstålet angriper altså resultanten av de jevnt fordelte spenningene midt i tverrsnittsflaten. For en sammensatt flate kan vi bestemme resultantens beliggenhet som følger:

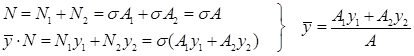
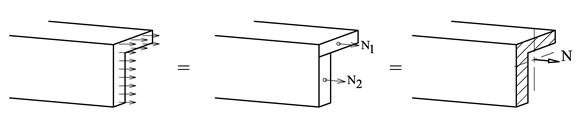
Vi legger merke til at resultantens beliggenhet utelukkende bestemmes av tverrsnittets geometri. Basert på det vi har vist over innfører vi derfor begrepet arealsenter som er definert som følger:

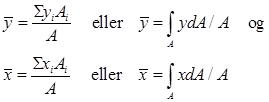
Uttrykkene kan betraktes som spesialtilfeller av momentteoremet, hvor det samlede arealets moment er lik summen av delarealenes momenter. Arealsenteret et fysisk punkt som ligger i snittflaten, og beliggenheten er uavhengig av hvilken akse som er referanse. Som vi har sett inngår areal og arealsenter i mange sammenhenger; vi bruker areal­betraktninger ved fordelte laster, i tyngdepunkts­beregninger og til å bestemme spenninger i bjelketverrsnitt.

Hvis vi ser bjelken fra siden blir arealsenteret er en akse som går gjennom bjelken. Det er en forutsetning for å få jevnt fordelte normalspenninger at normalkraften virker i bjelkeaksen. Figuren under viser en eksentrisk last som også gir bøyemoment i bjelken. Når normalkraften angriper utenfor arealsenteret så kan vi flytte normalkraften til arealsenteret hvis vi samtidig legger til et kraftpar.

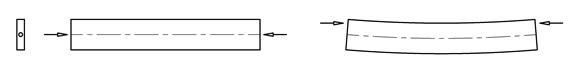
Som regel forutsetter vi at aksiallaster virker i bjelkeaksen, og bjelker tegnes gjerne som linjer uten utstrekning.