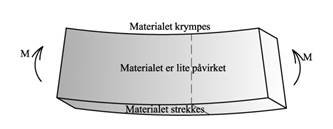
Figuren viser hvordan en bjelke som belastes med et bøyemoment deformeres. Bjelken får en krumning som gjør at undersiden av bjelken strekkes mens oversiden blir presset sammen, og et eller annet sted inni bjelken får vi en overgang fra strekk til trykk og her har vi ingen tøyning. Overgangen fra strekk til trykk skjer i en flate inni bjelken som kalles nøytralflaten og som går langs bjelken. Og hvis vi ser på et bjelketverrsnitt så finner vi denne flaten som en linje som vi kaller for nøytralaksen. Nøytralaksen er en linje i bjelketverrsnittet hvor det ikke er noen tøyning og dermed heller ingen normalspenninger.

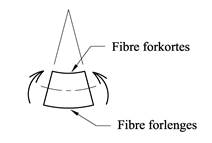
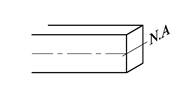
Det er vanlig å anta et bøyemoment ikke forvrenger bjelketversnittet, dvs. at et plant tverrsnitt forblir plant ved bøyning. Skjærkrefter vil gi en viss forvrengning av tverrsnittet men denne effekten er svært liten og som regel neglisjerbar. Antakelsen om at plane tverrsnitt forblir plane medfører at tøyningen av tverrsnittet vokser lineært i forhold til avstanden fra nøytralaksen. Så lenge materialet oppfører seg lineærelastisk vil i følge Hookes lov normalspenningene og tøyningene være proporsjonale størrelser, og bøyning gir dermed tøyninger og normalspenninger som vist under.

 

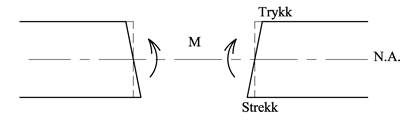
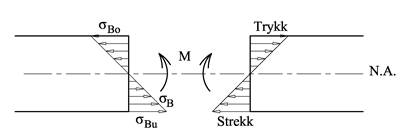
Bøyespenningene vokser proporsjonalt med avstanden fra nøytralaksen og at vi finner de største bøyespenningene i overkant og i underkant av tverrsnittet. Legg merke til at bøyespenningene er normalspenninger dvs. samme typen spenninger som for aksiallaster. I Meccanica vil vi bruke s_B for bøyespenninger og s_A for aksial­spenninger.

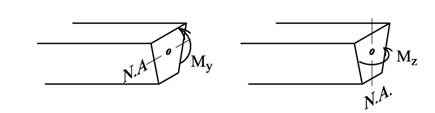
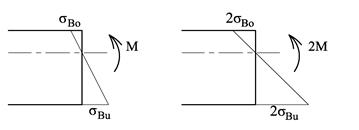
Nøytralaksen er den aksen som bøyemomentet virker om, og nøytralaksens orientering vil være avhengig av hvordan vi bøyer bjelken, jf. figur over. Og dersom det kun virker et bøyemoment på tverrsnittet vil nøytralaksen gå gjennom tverrsnittets arealsenter. For symmetriske tverrsnitt ligger nøytralaksen “i midten” og normalspenningene i overkant σ_Bo blir like store og motsatt rettet av normalspenningene i underkant σ_Bu. For usymmetriske tverrsnitt finner vi de største bøyespenningene på den siden som er lengst ifra nøytralaksen. Dette er illustrert i figuren under hvor σ_Bu er større enn σ_Bo. Arealsenterets beliggenhet har altså stor betydning for spenningsfordelingen.

                                Usymmetrisk                                                             Symmetrisk

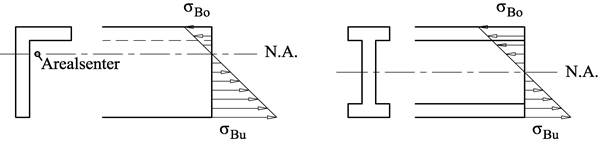
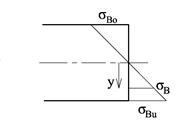
Vi skal vise at nøytralaksen for ren bøyning går gjennom arealsenteret. Figuren under viser en typisk spenningsfordeling over et bjelketverrsnitt med bøyemoment. Vi benevner spenningene i overkant og i underkant som henholdsvis σ_Bo og σ_Bu. Ved å plassere origo der hvor vi ikke har noen spenninger får vi et enkelt uttrykk for s som funksjon av y:

                                              

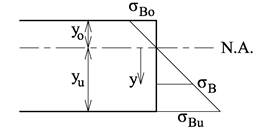
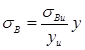
Vi har kun bøyning M og ingen normalkraft N på tverrsnittet dvs. at

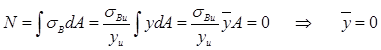
Avstanden fra nøytralaksen til arealsenteret er altså lik null. Dersom vi også har en normalkraft så vil , dvs. at det er en avstand fra nøytralaksen til arealsenteret. Normalkraften flytter altså nøytralaksen vekk fra arealsenteret.

Bøyespenningsformelen

Vi skal finne sammenhengen mellom bøyemoment og bøyespenninger og begynner med å se på en bjelke med rektangulært tverrsnitt. Dette kan f.eks. være en flattstålbjelke. Pga den enkle geometrien kan vi bruke trekantbetraktninger:

 

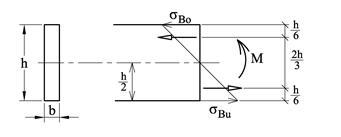
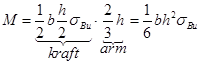
Hvis vi snur om på uttrykket får vi et uttrykk for de største spenningene:

Normalspenningene for et vilkårlig punkt i tverrsnittet blir:

Legg merke til bh³/12 og bh²/6 som er geometriske uttrykk for tverrsnittet. Vi skal nå se på den svært viktige bøyespenningsformelen som gir oss normal­spenningene for ethvert punkt i et bjelketverrsnitt som er belastet med bøyemomentet M.

σ_B    =     Normalspenningene i et bjelketverrsnitt som følge av et bøyemoment

M    =     Bøyemomentet som virker på snittet

y      =     Avstand fra nøytralaksen

I       =     Annet arealmoment av bjelketverrsnittet om nøytralaksen som bøyemomentet virker om

Bøyespennings­formelen gir oss normalspenningene på tverrsnittet, som funksjon av avstanden y fra nøytralaksen. Annet arealmoment er en rent geometrisk størrelse som uttrykker tverrsnittets motstand i forhold til bøyning. Vi ser at bøyemoment og bøyespenninger er proporsjonale størrelser.

Vi skal se hvordan bøyespenningsformelen framkommer. Figuren under viser et tverrsnitt som er utsatt for ren bøyning. Hvis vi legger origo i nøytralaksen får vi et enkelt uttrykk for normalspenningene σ_B:

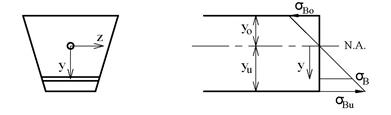
Hver liten del av tverrsnittet gir sitt lille moment­bidrag:

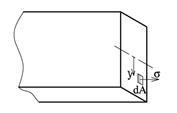
Når vi integrerer dette momentet over hele tverrsnittflaten får vi resultantmomentet M:

Vi ønsker et uttrykk for normalspenningene og vi snur derfor om på uttrykket og får: