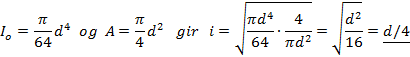Dersom vi belaster en lang og tynn stav med en trykkraft så kan vi oppleve at staven plutselig blir ustabil og bøyer ut. Staven mister sin styrke og vi får store elastiske deformasjoner. Fenomenet kalles knekking og er en form for konstruksjonssvikt som kjennetegnes ved at et konstruksjonselement som er påkjent med trykkraft plutselig kollapser, og dette skjer til tross for at trykkspenningene ligger langt under materialets flytegrense. Knekking er vanligvis sterkt uønsket.
Prøv selv med en linjal el.l. Vi skjønner umiddelbart at knekking først og fremst er et problem for lange og tynne konstruksjoner som er belastet med en trykkraft. Legg merke til at linjalen alltid knekker ut om sin svakeste akse. Ved knekking bøyer elementet plutselig ut sideveis og mister bæreevnen. Dette er en elastisk deformasjon, og elementet går tilbake til sin opprinnelige form hvis vi fjerner lasten. Elementet har blitt ustabilt selv om materialet er upåvirket og vi sier at knekking er et stabilitetsproblem. Elastisk knekking oppstår dersom den ytre kraften overstiger knekklasten, og for slanke elementer kan knekklasten uttrykkes ved følgende enkle formel:
![]()
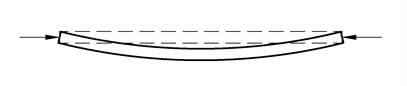
FE kalles for eulerlasten. Uttrykket EIo kalles for bøyestivheten og inngår i alle formler som omhandler utbøyning. Bortsett fra E-modulen er det ingen materialegenskaper i formelen, og det betyr at høyfast stål ikke er sterkere enn vanlig konstruksjonsstål med hensyn til knekking. Men for aluminium blir knekklasten bare en tredjedel på grunn av lav E-modul. Elementet knekker alltid ut om tverrsnittets svakeste akse og det betyr at vi skal bruke annet arealmoment om tverrsnittets svake akse i formelen. Sirkulære tverrsnitt har ingen sterk eller svak akse og her er det vilkårlig hvilken retning elementet knekker ut. I formelen inngår knekklengden Lk som er elementets effektive lengde hvor vi tar hensyn til opplagerbetingelser. Knekklengden er avstanden mellom punkter hvor kurvaturen skifter retning. Figuren under viser knekklengden for fire typer opplagring.
Vi har altså en enkel formel for å bestemme knekklasten. Vi ser at det er de slanke elementene, dvs. lange og tynne elementer med liten Io og stor Lk som knekker først ut når de blir trykkpåkjent. Og så vet vi at korte og kompakte elementer aldri knekker ut, slike elementer får i stedet plastisk deformasjon.
Slankhet er et sentralt begrep i knekking som er definert som forholdet mellom knekklengde og treghetsradius
Slankhet:
![]()
Treghetsradius:
![]()
Treghetsradien er et karakteristisk mål på elementets bredde og er definert som vist over. Io er tverrsnittets minste annet arealmoment mens A er tverrsnittsareal. Vi kan regne ut treghetsradien eller vi kan finne tverrsnittets treghetsradius i profiltabeller. Vi kan nå sette opp et uttrykk for den elastiske knekkspenningen som funksjon av slankheten:
Eulerspenning:
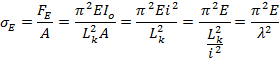
Slankheten λ er den eneste geometriske størrelsen som inngår i formelen, og jo lengre og tynnere element desto lettere knekker elementet ut. Diagrammet under viser knekkspenningen som funksjon av slankhet for stål. Vi ser at kapasiteten blir svært lav for de slankeste elementene, mens de kompakte elementene får svært stor kapasitet.

Eulerspenningen er en teoretisk formel som ikke tar hensyn til materialegenskapene, og for kompakte elementer vil eulerspenningen overskride flytegrensen. Dette er urealistisk, i praksis vil alle trykkstaver knekke ut når materialspenningene nærmer seg flytegrensen. Flytegrensen påvirker knekkapasiteten, og erfaringer viser at vi ikke bør bruke eulerspenningen når denne overstiger halve flytegrensen. Med utgangspunkt i S355 regner vi ut hvilken slankhet som gir eulerspenning lik henholdsvis flytegrensen (σE = Re) og halve flytegrensen (σE = Re/2):
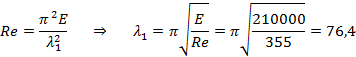
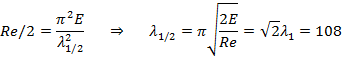
Legg merke til at λ1og λ1/2 er materialkonstanter som angir overgangen mellom elastisk og plastisk knekking. λ1/2 angir grensen for når σE kan brukes. Relativ slankhet er et begrep som benyttes for å klassifisere elementer i forhold til λ1 og brukes for å bestemme om det er elastisk eller plastisk knekking som er relevant.
Relativ slankhet:
![]()
Teoretisk kunne man tenke seg at for elementer som er slankere enn λ1 så får vi elastisk knekking mens hvis slankheten er mindre enn λ1 så får vi flytning. Men for mellomslanke elementer får vi såkalt plastisk knekking som opptrer før vi når både flytegrensen og den elastiske eulerspenningen. Kapasiteten for mellomslanke elementer dvs. elementer med slankhet i nærheten av λ1 lar seg best beskrive med empiriske formler. Vi skal her vise en metode med kurvetilpasning for å beregne knekkapasiteten for mellomslanke elementer. Følgende formel er en parabel som går gjennom punktene σk = Re ved λ = 0 og σk = Re/2 ved λ = λ1/2.
Plastisk knekking:
![]()
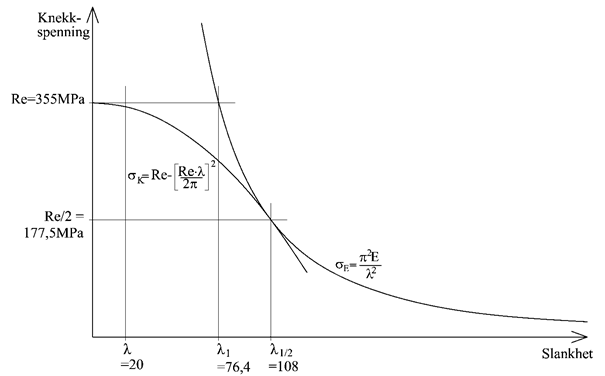
For elementer med liten slankhet, typisk λ < 20, blir knekkspenningen tilnærmet lik flytegrensen. λ kan brukes for å klassifisere konstruksjonselementer i forhold til om vi får plastisk eller elastisk knekking. Figuren under illustrerer hvordan tverrsnittet (evt. knekklengden) påvirker svikttypen.
λ > 108 20<λ<108 λ<20
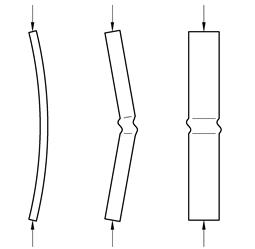
For korte og tykke elementer vil knekkspenningen bli så stor at den overstiger flytegrensen og knekning blir dermed ikke dimensjonerende. For mellomslanke elementer kan vi få såkalt plastisk knekning som er en mellomting mellom flytning og knekning, dvs. en ustabilitet som medfører plastisk deformasjon. Hvis slankheten er under 10 så er knekking ikke et problem.Når et element knekker ut, mister det brått sin bæreevne og vi har derfor liten reststyrke, og det er derfor vanlig med stor sikkerhetsfaktor i forhold til knekking. Vi skal være obs på at knekning kan være et større problem for konstruksjoner av høyfast stål. Dette skyldes at vi tillater høyere spenninger og dermed slankere konstruksjoner.
Eksempel
Beregn treghetsradius for rektangulært og sirkulært massivt tverrsnitt
Rektangel:
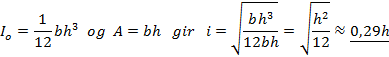
Sirkel: