Normalspenninger

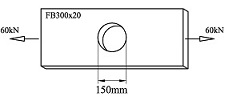
Figuren viser en fastholdt stav hvor det virker en strekkraft i den ene enden. Vi skjønner utfra likevektskravene at det virker en like stor og motsatt rettet kraft i enden hvor staven er fastholdt. En stav som utsettes for strekk er altså belastet med aksiallaster i hver ende. Hvis vi vil vite hvilke krefter som virker inni staven når den strekkes må vi tenke oss et snitt som deler staven i to. For at hver halvdel skal være i likevekt må det virke en normalkraft N på snittet. De to normalkreftene virker på hver sin halvdel og er motkrefter til hverandre.

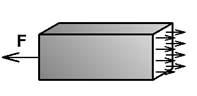
Normalkraften som virker i snittet er ikke egentlig en punktlast. I og med at hele stavens tverrsnitt strekkes er det naturlig å anta at normalkraften fordeler seg jevnt over snittet. Figuren under viser hvordan strekkrefter inni en stav egentlig ser ut.

Vi innfører et begrepet normalspenninger som er det samme som kraft per arealenhet. Vi bruker symbolet σ (sigma) for normalspenninger. Vi bruker gjerne enheten mm² for en bjelkes tverrsnittsareal og dermed får normalspenninger enheten N/mm² som er det samme som MPa (Mega-Pascal). Materialspenninger har en del fellestrekk med trykk som også har enheten kraft per arealenhet. Normalspenningene og normalkraften er to sider av samme sak; normalspenningene beskriver det som skjer for hver fiber i materialet mens normalkraften N er resultanten av disse normalspenningene. Både normalspenningene og normalkraften virker normalt på snittet, derav navnet. Vi kan sette opp følgende enkle uttrykk for normalspenningene hvor indeks A betyr at det er normalspenninger pga en aksialkraft., dvs en kraft som virker i bjelkens lengderetning.

Normalkraftens angrepspunkt

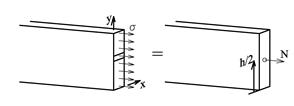
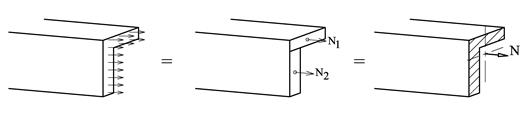
Figuren viser tverrsnittet av et flattstål hvor det virker normalspenninger som er jevnt fordelt. Konstant σ gir normalkraften N = σ A. Momentet for en liten del av snittet blir dM = yσdA. Normalkraftens beliggenhet i forhold til x-aksen bestemmes med momentteoremet:

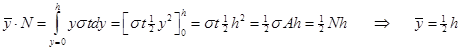
På tilsvarende vis kan vi finne beliggenheten i forhold til y-aksen som . Legg merke til at beliggenheten bestemmes utelukkende ut fra tverrsnittets geometri. Resultanten av de jevnt fordelte spenningene angriper midt i tverrsnittsflaten, i et punkt som vi kaller for arealsenteret. Resultantens beliggenhet for en sammensatt flate bestemmes på tilsvarende vis:

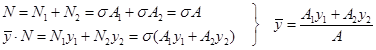
Også her er resultantens beliggenhet en rent geometrisk størrelse. Vi innfører begrepet arealsenter som følger:

eller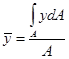

Uttrykkene kan betraktes som en variant av momentteoremet, hvor totalarealets moment er lik summen av enkeltarealenes momenter om enhver akse. Uttrykkene over viser arealsenterets beliggenhet i forhold til y-aksen. Arealsenterets avstand til y-aksen kan vi finne på tilsvarende vis.

Vi har vist at resultanten av jevnt fordelte spenninger på et bjelketverrsnitt angriper i snittets arealsenter. For en bjelke danner tverrsnittets arealsenter en akse i bjelkens lengderetning, og vi kaller denne for bjelkeaksen. En forutsetning for at en aksialkraft skal gi jevnt fordelte normalspenninger er at aksialkraften angriper i bjelkeaksen. Hvis aksiallasten angriper utenfor arealsenteret vil vi både få normalkraft og bøyemoment i bjelken er det derfor en forutsetning at aksiallasten angriper i bjelkeaksen. Vær obs på at vi i dette faget betrakter bjelkeelementene som en linje uten utstrekning. Resultanten av normalspenningene på en snittflate vil typisk bli en normalkraft i arealsenteret pluss et bøyemoment.

 

Tøyning

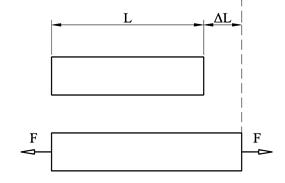
Mange materialer er elastiske, dvs. at hvis vi påfører en strekkraft på en stav, så vil staven forlenges. Og med en trykkraft blir staven kortere. Staven over har lengden L og får forlengelsen ΔL pga. strekkraften. Vi innfører begrepet tøyning som er det samme som relativ forlengelse og som er definert som følger:

Tøyning er en dimensjonsløs størrelse. Tøyningen kan enten være elastisk, og det betyr at materialet går tilbake til sin opprinnelige form når vi tar bort kraften, eller tøyningen kan være plastisk, dvs. at vi får en varig deformasjon.

Som vi skal se i materialegenskaper er det mange konstruksjonsmaterialer som oppfører seg lineærelastisk så lenge materialspenningene ikke er så store at materialet ødelegges. Staven oppfører seg som en svært stiv fjær og forlengelsen øker proporsjonalt med strekkraften, dvs. ΔL = F/k, hvor proporsjonalitetskonstanten k er fjærstivheten.

Fjærstivheten, slik den er vist over, gjelder for en konkret stav, med gitt tverrsnitt, lengde og materiale. Vi ønsker en fjærstivhet som sier noe om materialet og som er uavhengig av stavens dimensjoner. Hvis ΔL og F er proporsjonale størrelser så må også σ og ε være proporsjonale størrelser. Vi setter opp Hookes lov som gir oss sammenhengen mellom spenning og tøyning for lineærelastiske materialer:

σ = Eε

E er en materialkonstant som kalles elastisitetsmodul eller bare E-modul (engelsk: Young's modulus). De viktigste verdiene for E er:

E_stål = 206000MPa og E_Alum = 70000MPa

Vi kan nå sette opp et uttrykk for forlengelsen av en aksialbelastet stav.

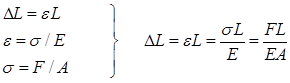
Det anbefales å gjøre alle enheter om til mm når man skal beregne forlengelse.

Temperaturtøyning

De fleste materialer utvider seg ved økende temperatur og vi kan bruke følgende enkle uttrykk for dette fenomenet:

.

α er materialets lengdeutvidelseskoeffisient, og som vi ser har denne en litt spesiell enhet. En bjelke med lengden L som varmes opp, får forlengelsen . Forlengelsen er altså proporsjonal med temperaturøkningen. Legg merke til at aluminium er mer følsom overfor temperaturendringer enn stål.

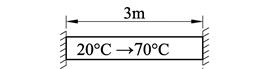
Hva skjer dersom en stålbjelke er fast innspent i begge ender varmes opp? Vi bruker superposisjonsprinsippet og antar først at stålbjelken får utvide seg fritt:

(1).

Deretter presser vi bjelken tilbake til opprinnelig lengde.

Vi kan få svært store temperaturspenninger i konstruksjoner som er forhindret fra å utvide seg. Vi kan sette opp uttrykket for temperaturspenningene direkte. Forlengelsen fra temperaturøkning er lik forkortelsen fra sammenpresningen dvs. eller og vi får

Eksempler

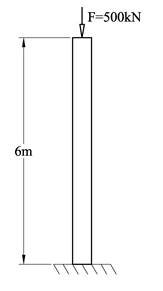
Skråstag

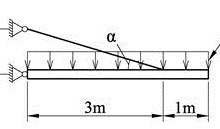
Plate med utkapp