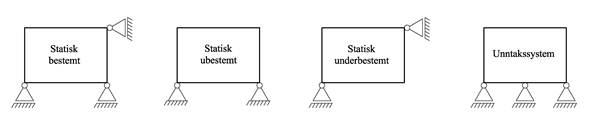
I og med at vi bare har tre uavhengige likevektslikninger, kan vi bare bestemme tre ukjente størrelser på en konstruksjon. Vi sier at konstruksjonen er statisk bestemt hvis den er opplagret på en slik måte at alle ukjente størrelser lar seg bestemme vha likevektslikningene.

Hvis antall ukjente størrelser er større enn antallet tilgjengelige likevektslikninger, sier vi at konstruksjonen er statisk ubestemt. For å løse de statisk ubestemte problemene, må vi supplere likevektslikningene med tilleggsbetingelser hvor vi tar hensyn til deformasjoner. Vi skal se nærmere på dette i slutten av kurset.

En konstruksjon med flere likevektslikninger enn antallet ukjente sier vi er statisk underbestemt. Slike konstruksjoner kan ikke bære en vilkårlig belastning.

Systemer hvor antall ukjente reaksjonskrefter er lik antall likevektslikninger men hvor legemet likevel ikke kan bære en vilkårlig belastning kalles unntakssystemer.

En statisk bestemt konstruksjon kjennetegnes av at den er opplagret på en slik måte at den er akkurat fastholdt. I Meccanica skal vi stort sett bare forholde oss til statisk bestemte konstruksjoner.

Statisk bestemthet for konstruksjoner

Figuren under viser en ramme hvor to bjelker er forbundet i et bolteledd. Konstruksjonen har 4 ukjente opplagerkrefter (A_x, A_y, C_x og C_y). For hele konstruksjonen kan vi bare sette opp tre uavhengige likevektslikninger. Betyr dette at konstruksjonen er statisk ubestemt? Hvis vi fjerner en av opplagerbetingelsene vil vi få en konstruksjon som ikke er i stand til å bære en vilkårlig last. Betyr dette at konstruksjonen er statisk bestemt?

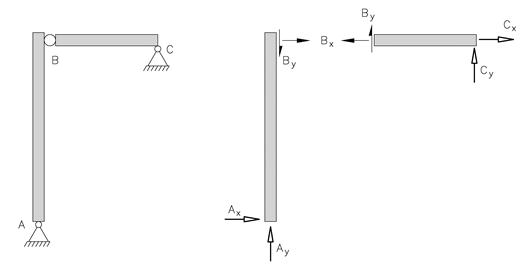
Dersom vi deler konstruksjonen i to ved leddet må vi erstatte leddet med to nye ukjente krefter som virker mellom de to elementene. Vi teller opp og ser at på elementnivå får vi i alt 6 ukjente reaksjonskrefter. Vi kan sette opp tre likevektslikninger for hvert element så lenge vi også tar med de nye leddkreftene, og vi får totalt 2·3=6 likevektslikninger. Vi har altså fått en situasjon med 6 ukjente og 6 likninger og det betyr at konstruksjonen er statisk bestemt. Legg merke til at når vi deler en konstruksjon i to ved et ledd får vi to nye ukjente mens vi får tre nye likninger. Vi "vinner" altså en likning.

Vi har tidligere lært at vi har tre uavhengige likevektslikninger. Egentlig har vi tre uavhengige likevektslikninger per element. En konstruksjon er statisk bestemt hvis

3e = r, e = antall elementer, r = antall ukjente reaksjonskrefter

Vi skal undersøke om rammen under er statisk bestemt. På konstruksjonsnivå har vi tre ukjente reaksjonskrefter (A_x, A_y og C_y). Vi kan sette opp tre uavhengige likevektslikninger for hele konstruksjonen, dvs at konstruksjonen er statisk bestemt.

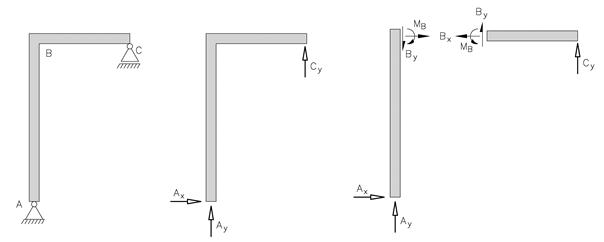
Hva om vi betrakter konstruksjonen på elementnivå? Når vi deler en konstruksjon i to ved en fast innspenning får vi tre nye ukjente og tre nye likevektslikninger, dvs. det blir ingen endring mht statisk bestemthet (e = 2 og r = 6 gir 3e = r).

Rammer

En konstruksjon som er bygget opp av flere bjelker kalles gjerne en ramme. Under er det vist fire rammer som alle er statisk bestemt på konstruksjonsnivå. Hvis vi derimot ønsker å bestemme kreftene som virker på det enkelte element, er det bare de to i midten som er statisk bestemt.

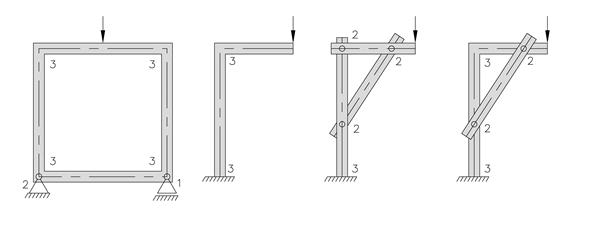
e = 4	e = 2	e = 3	e = 3
r = 15>	r = 6	r = 9	r = 10
3e < r	3e = r	3e = r	3e < r
Statisk ubestemt	Statisk bestemt	Statisk bestemt	Statisk ubestemt

 

Legg merke til skråstagene i rammene over som er leddet i hver ende. Det virker ingen last direkte på skråstagene, all belastning skjer via leddene. Dette er eksempler på aksialstaver.

Eksempel

Sjekk om konstruksjonene er statisk bestemt

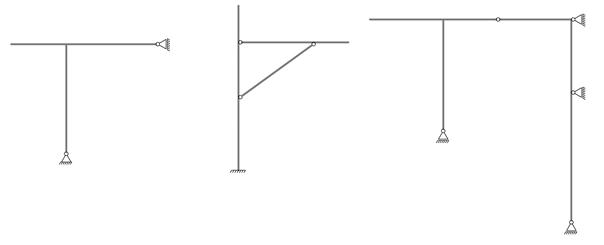
e = 2 r = 6

e = 3 r = 9

e = 4 r = 12