Eksempel (grunnleggende)

Bestem skjærkraft og bøyemoment for et vilkårlig tverrsnitt av bjelken og sett opp skjærkraft- og bøyemomentdiagram.

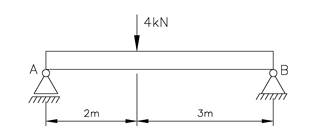
Løsning

Vi setter opp belastningsdiagram direkte uten å vise utregningen:

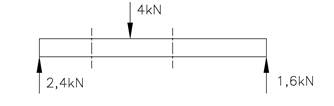
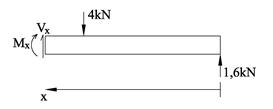
Vi begynner med å kartlegge snittkreftene mellom første og andre punktlast, fra venstre. Når vi skal bestemme snittkreftene deler vi konstruksjonen i to ved posisjonen x og x ligger et vilkårlig sted mellom første og andre punktlast, dvs. x Î <0,2>. Vi tegner et FLD for venstre halvdel hvor både ytre krefter og de ukjente snittkreftene V_x og M_x er med. Snittkreftene tegnes med positiv retning, jf. fortegnsreglene.

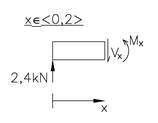
Vi bestemmer snittkreftene vha. likevektslikninger. Her er valg av positiv retning vilkårlig.

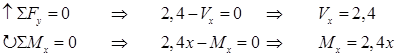
Legg merke til at momentpunktet i momentlikningen ligger i snittet. Dermed unngår vi at V gir noe momentbidrag. Momentet vokser lineært i intervallet <0,2> og vi behøver bare å regne ut verdier ved endene.

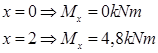
Deretter finner vi snittkreftene mellom andre og tredje punktlast. Vi legger inn et nytt snitt på et vilkårlig sted mellom andre og tredje punktlast, dvs x Î <2,5>. Vi tegner FLD for venstre halvdel og bestemmer snittkreftene vha likevektslikninger.

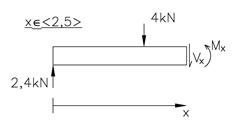
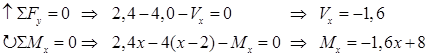
Bestemmer momentets verdi ved hver ende av intervallet:

            x = 2  Þ  M_x = 8 – 3,2 = 4,8kNm

x = 5  Þ  M_x = 8 – 1,6∙5 = 0kNm

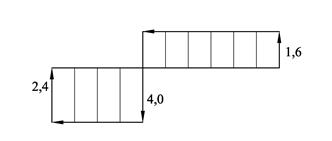
Negetiv V_x betyr at skjærkraften vender oppover. Legg merke til at V_x er lik summen av ytre tverrkrefter og M_x er lik summen av ytre momenter om x. Vi kan skrive #ΣF_y = $V_x og PΣM_ytre = QM_snitt. Vi er omsider klar for å sette opp skjærkraft- og bøyemomentdiagram.

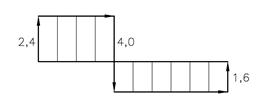
Diagrammene viser hvordan V og M varierer langs bjelken, og diagrammene skal tegnes normalt på elementet. Vi fyller diagrammet med linjer for å vise hvilket element diagrammet tilhører. Tegn gjerne selve elementet med annen farge. Legg merke til at V-diagrammet har konstant verdi og at M-diagrammet varierer lineært mellom punktlastene. Legg også merke til at det ikke er noe moment ved endene, og dette skyldes at bjelken er fritt opplagret og det skjer ingen momentoverføring. Vi ser av dette at det er tilstrekkelig å beregne bøyemomentet ved punktlastene når vi skal tegne M-diagrammet. Legg merke til at V-diagrammet enkelt kan tegnes fra venstre mot høyre ved å følge kraftpilene.

Det er valgfritt hvilken side av elementet skjærkraften skal tegnes på. Men momentdiagrammet tegnes alltid på strekksiden, i dette tilfellet undersiden. Dermed gir moment­diagrammet et visuelt bilde av belastningen. Det er spesielt bøyemomentet som gir store belastninger på materialet og som er avgjørende for valg av bjelkedimensjoner. Legg merke til at vi finner det største bøyemomentet rett under punktlasten. Det dimensjonerende bøyemoment blir M_dim = 4,8kNm, forutsatt at bjelken har konstant tverrsnitt.

Vi kunne også brukt høyre del for å bestemme snittkreftene, og det hadde vel vært noe enklere for intervallet mellom andre og tredje punktlast. Uttrykkene blir forskjellige men de representerer samme diagram. I noen tilfeller er det gunstig å regne seg innover mot midten, både fra høyre og fra venstre.

Vi forsøker å gå fra høyre:

x Î <0,3>:

                    

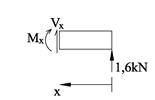
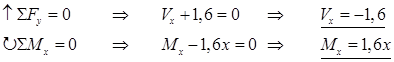
x Î <3,5>:

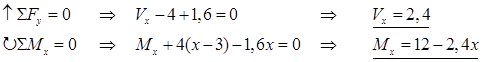
Legg merke til at når vi følger kraftpiler og går fra høyre mot venstre, så havner skjærkraftdiagrammet på andre siden av elementet.