Konstruksjoner som utelukkende er bygd opp av aksialstaver kalles fagverk. Fagverk er en konstruksjonstype som er mye brukt fordi den utnytter materialet på en svært effektiv måte. Generelt er aksiallaster langt å foretrekke framfor bøyemomenter. Vi husker at et element som er leddet i hver ende og som kun er belastet i leddene blir en aksialstav, dvs. at elementet kun får trykk eller strekk; bøyemoment og skjærkraft er ikke mulig. Derfor er ledd viktig når vi skal konstruere et fagverk. Det ideelle fagverk er en konstruksjon som består av staver som er forbundet med hverandre i ledd (kalles for knutepunkt eller noder), og alle ytre krefter virker i leddene. Men hvordan kan en konstruksjon med ledd fungere som en bærende konstruksjon? Da er vi avhengig av å bruke trekanter. Hvorfor?

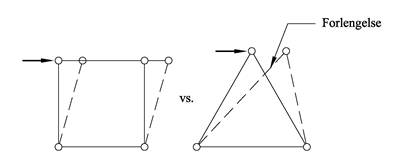
Fagverkene er lett å kjenne igjen fordi de er sammensatt av trekanter, og vi finner fagverk i bruer, takstoler, tårnkraner osv. Et fagverk er egentlig en tredimensjonal konstruksjon men i dette emnet skal vi bare se på plane fagverk som egentlig vil være ustabile. I praksis vil ikke noen konstruksjoner fullt ut tilfredsstille kravene til det ideelle fagverk; vi må bl.a. se bort fra konstruksjonens egenvekt som jo er jevnt fordelt. Og i dag er de fleste forbindelser sveiset og ikke leddet, men så lenge stavaksene har felles skjæringspunkt gjør vi liten feil om vi neglisjerer innspenningskreftene. I tillegg til å være en svært sterk og materialeffektiv konstruksjon har fagverket også beregningsmessige fortrinn som gjør at vi kan bestemme kreftene selv på komplekse konstruksjoner. En typisk fagverksoppgave omfatter å vurdere statisk bestemthet, bestemme opplagerkrefter og å bestemme stavkrefter, og vi har to metoder for å beregne stavkrefter i fagverk.

Knutepunktsmetoden

Denne metoden egner seg spesielt for enkle fagverk hvor vi skal beregne alle stavkreftene. Vi setter opp et såkalt knutepunktsdiagram som er et fritt-legeme-diagram hvor bare fagverkets knutepunkter er tegnet inn og hvor stavene er erstattet med de ukjente stavkreftene. I og med at vi kun får en ukjent størrelse (aksiallasten) per stav gir en slik fremstilling oss en fin oversikt over samtlige ukjente størrelser i konstruksjonen. Legg merke til hvordan stavkreftene navngis; S_AD er f.eks. aksialkraften i staven mellom knutepunkt A og D.

Konstruksjon

Knutepunktsdiagram

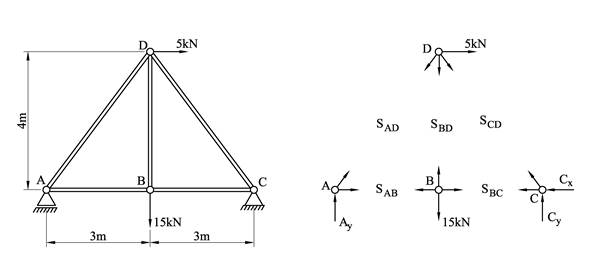
Her som ellers i statikk er fortegn viktige, dvs. har vi strekk eller trykk? Vi definerer strekk som positiv og trykk som negativ aksiallast. I fagverk får vi gjerne mange ukjente størrelser og det er vanskelig å vite om man får trykk eller strekk. Når vi setter opp knutepunktsdiagrammet antar vi derfor strekk i alle staver. En vanlig feil er å tegne strekkreftene med pilen feil vei. Husk på at strekk i staven også gir strekk i knutepunktet.

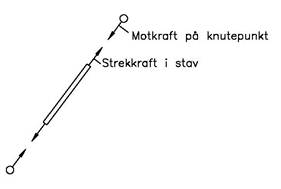
Når knutepunktsdiagrammet er satt opp kan stavkreftene bestemmes ved å sette opp likevektsuttrykk for det enkelte knutepunkt. Kreftene som virker på et knutepunkt er sammenløpende og vi har derfor bare to likevektslikninger for hvert knutepunkt. Opplagerkreftene kan bestemmes ut fra likevektskrav for hele fagverket får man beregner stavkreftene. Likevektslikningene for det siste knutepunktet vil i så fall bare bli en sjekk på om vi har regnet riktig.

Snittmetoden

For fagverk med mange elementer hvor vi bare er interessert i å bestemme noen få stavkrefter bruker vi en metode som kalles snittmetoden. Vi kan alltid sette opp likevektslikninger for hele konstruksjonen, for et element, for et knutepunkt eller for deler av en konstruksjon, og det er det siste vi benytter oss av i snittmetoden. I snittmetoden deler vi konstruksjonen i to ved å legge inn et snitt som går gjennom de stavene som skal bestemmes. Stavkreftene mister sin motkraft og blir dermed ytre krefter som må tas med i kraftregnskapet.

Statisk bestemthet

Vi husker at statisk bestemthet handler om å sjekke om konstruksjonen har like mange likevektslikninger som antall ukjente krefter. Et fagverk har en ukjent størrelse per stav pluss opplagerkreftene, mens vi har to likevektslikninger per knutepunkt til disposisjon. Vi kan derfor sette opp følgende forenklete uttrykk for statisk bestemthet for fagverk:

s + o = 2k hvor	s = antall staver
	o = antall opplagerkrefter
	k = antall knutepunkt