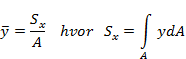Tyngdepunkt

Tyngden til et objekt kan uttrykkes ved materialets egenvekt og legemets volum som G = ρgV, såfremt materialet er homogent, dvs at materialet har de samme egenskapene gjennom hele objektet. Dersom objektet har enkel geometri så har vi egne formler for å beregne objektets volum. De viktigste konstruksjonsmaterialene er stål med egenvekt ρ_stål = 7,85t/m³ og aluminium med ρ_al = 2,7t/m³. Tyngden til et objekt er egentlig resultanten av en lang rekke små tyngdekrefter som fordeler seg utover materialet i objektet.

Med begrepet tyngdepunkt mener vi punktet hvor legemets resultanttyngde angriper, og resultanttyngden går gjennom tyngdepunktet uansett hvordan legemet er orientert i forhold til tyngdefeltet. I praksis vil gjerne kraftfeltet hvor legemet befinner seg være konstant og dermed sammenfaller tyngde­punktet med legemets massesenter. Og hvis legemets materiale er homogent så sammenfaller tyngdepunktet med volumsenteret. For objekter med enkel geometri har vi egne formler for å bestemme tyngdepunktets plassering, for rektangulære objekter får vi f.eks.

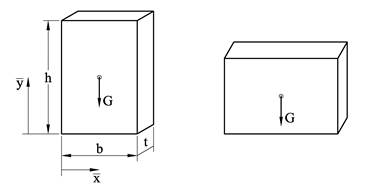
Tyngdepunktets plassering angis i forhold til et referansepunkt. Egentlig virker det en liten tyngdekraft på hver liten partikkel i legemet og legemets totale tyngde er kraftresultanten av G₁, G₂ osv. I og med at de fordelte kreftene er parallelle, kan vi addere disse sammen uten videre og finne tyngden som G = ΣG_i. Tyngdens beliggenhet bestemmes med momentteoremet som sier at resultantens moment skal være lik summen av enkeltkreftenes momenter om ethvert punkt P, dvs. .

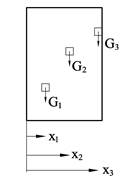
Vi får den viktige tyngdepunktssetningen som brukes for å bestemme tyngdepunktets beliggenhet for sammensatte legemer. For ordens skyld har vi også tatt med det generelle uttrykket for tyngdepunkt hvor det integreres over hele volumet. Tilsvarende uttrykk kan settes opp for

,    ,   

 

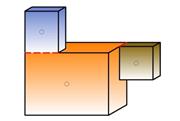
Når tyngdens akselerasjon g er konstant kan denne reduseres bort og det betyr at det ikke spiller noen rolle om vi regner i kg eller i N. Hvis materialet dessuten er homogent kan også egenvekten reduseres bort og tyngdepunktet kan bestemmes utelukkende ut fra legemets volumgeometri.

 

 

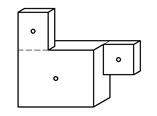
Hvis legemet har konstant tykkelse kan tyngdepunktet bestemmes utelukkende ut fra arealbetraktninger og vi kan betrakte legemet to-dimensjonalt:

 

 

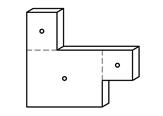
Uttrykkene og kaller vi for hhv. volumsenter og arealsenter. I mekanikk bruker vi gjerne arealbetraktninger for å bestemme resultanten av krefter som er jevnt fordelt over en flate, og resultantens beliggenhet sammenfaller da med arealsenteret.

Flategeometri

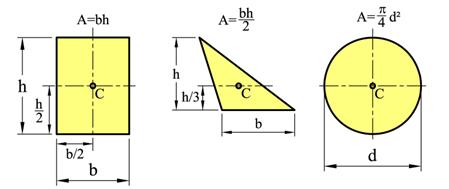
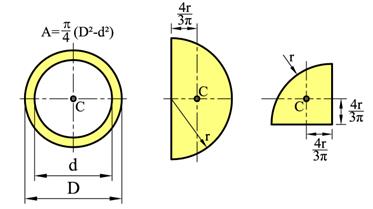
På tilsvarende vis som vi kan finne tyngden og tyngdepunktet til et legeme kan vi også finne areal og arealsenter til todimensjonale flater. I figuren over er det angitt arealformler for noen enkle geometriske flater og hvor arealsenteret befinner seg. Beregning av areal og arealsenter er et nyttig hjelpemiddel i sammenhenger hvor vi skal bestemme resultanten av parallelle krefter, og vi kan benytte arealbetraktninger for å gjøre fordelte laster om til punktlaster, for å beregne tyngde og tyngdepunkt for objekter, og når vi skal finne sammenhenger mellom spenninger og snittkrefter. Vi skal her se hvordan areal og arealsenter bestemmes, uavhengig av anvendelsesområdet.

              

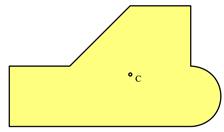
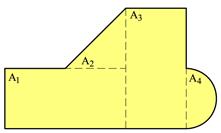
Når vi skal finne arealet av en flate som vist i figuren over, stykkes flaten opp i et endelig antall delflater og vi finner flatens totale areal ved å legge sammen delarealene, dvs. A_TOT = ΣA_i. Når vi skal finne arealsenterets beliggenhet innfører vi et koordinatsystem, vi velger origo og orienterer x- og y-aksen i forhold til geometrien.

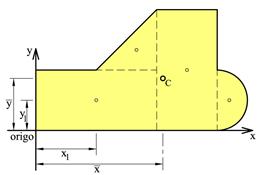
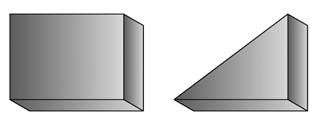
Arealsenteret er definert som følger:

S_y og S_x er “første arealmoment” om henholdsvis y-aksen og x-aksen. Formlene forutsetter at vi kan dele flaten inn et endelig antall deflater. Dersom dette ikke er tilfelle må vi integrere og formlene for areal og arealsenter blir som følger: