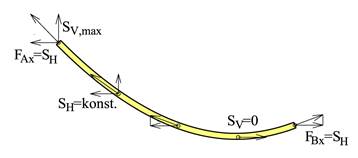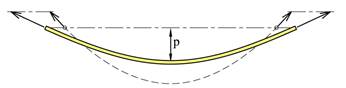
Dersom det henger en kjetting, en kabel eller et tau mellom to forankringspunkter så får denne en form omtrent som vist over. På grunn av kabelens egenvekt får kabelen et nedheng med en tilnærmet parabelform. I tilfellet over hvor forankringspunktene ligger på samme høyde er nedhenget symmetrisk. I hver ende virker forankringskreftene som har samme retning som selve kabelen. Og hvis vi trekker de to endene utover vil forankringskreftene øke, etter hvert som nedhenget minker. Vertikalkomponenten av forankringskraften skal bare utligne kabelvekten og er derfor den samme, uavhengig av kabelstrekket. Horisontalkomponenten er derimot omvendt proposjonal med nedhenget og ved små nedheng kan denne bli svært stor. Det går strekkrefter gjennom hele kabelen og strekket har samme retning som selve kabelen. Strekkets horisontalkomponent er konstant gjennom hele kabelens lengde og det betyr at vi får det største trekket der hvor kabelen er brattest, dvs. ved forankringspunktene. For symmetriske kabler får vi følgende kabelstrekk:
Horisontalstrekk: ![]() =
konstant gjennom hele kabelen
=
konstant gjennom hele kabelen
Kabelstrekk: ![]() =
størst der hvor kabelen er brattest dvs. ved endene
=
størst der hvor kabelen er brattest dvs. ved endene
Figuren under viser det generelle tilfellet hvor forankringspunktene har forskjellig høyde. Nedhenget uttrykkes ved pilhøyden p som er vertikalavstanden mellom kabelen og den rette linjen mellom opphengspunktene A og B, på midten. Spennvidden L er horisontalavstanden mellom A og B mens h er høydeforskjellen.
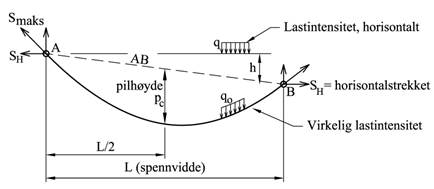
For små nedheng, dvs. når strekket er langt større enn kabelens egenvekt, kan kabellengden tilnærmet bestemmes som:
![]()
Egentyngden gjør at kabelen belastes med en lastintensitet qo som er konstant langs kabelen. Lastintensiteten horisontalt q blir dermed større jo brattere kabelen er. Det er komplisert å beregne den korrekte lastintensiteten og vi gjør derfor en forenkling og antar at lastintensiteten horisontalt q er konstant. Når kabellengden s er kjent kan vi bruke lastintensiteten q = qos/L hvor qo er egentyngden per meter kabel. Ved små nedheng (p/l < 1/5) kan vi bruke q = qo AB/L. Fritt-legeme-diagrammet for en kabel blir da typisk som følger:
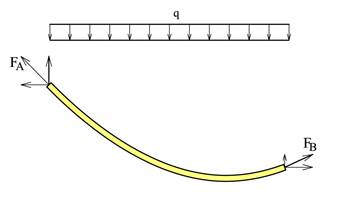
I og med at vi kun har vertikallast blir horisontalstrekket i hver ende likt og dette gjelder uansett hvilken del av kabelen vi ser på. Horisontalstrekket er altså konstant og vi kaller denne for SH, og i kabelens bunnpunkt har vi kun horisontalstrekk. Vi antar at kabelen ikke har noen bøyemotstand og strekkreftene følger kabelretningen. Dermed får vi størst strekk der hvor kabelen er brattest dvs. i opphengspunktene. Forankringskraften i opphengspunktene er en viktig størrelse og det er spesielt disse vi er interessert i å bestemme.