Fram til nå har vi sett på svært enkle konstruksjoner. Vi skal nå ta for oss plane konstruksjoner som er satt sammen av flere konstruksjonselementer, og en typisk problemstilling vil være å bestemme reaksjonskreftene som virker mellom de enkelte elementene. For å forstå de sammensatte konstruksjonene må vi først se på begrepene kraft og motkraft og indre og ytre krefter.

Kraft og motkraft

Krefter opptrer alltid parvis som en gjensidig påvirkning mellom to legemer og Newtons 3. lov slår fast at disse to kreftene dvs. kraft og motkraft er like store men motsatt rettet. Dette betyr at for alle krefter som virker på et legeme vil det alltid finnes en er like stor og motsatt rettet motkraft som virker på et annet legeme.

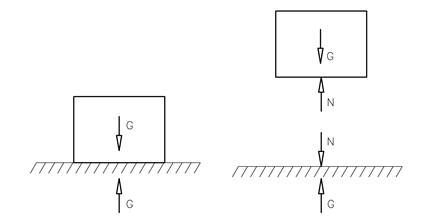
Figuren viser en kloss med tyngden G som ligger i ro på bakken. På underlaget virker en tilsvarende motkraft G oppover. Klossen er i statisk likevekt. Dette skyldes at det i kontaktflaten mot underlaget virker en normalkraft N oppover på klossen som er like stor som G og motsatt rettet.  Kraftsystemet på klossen består altså av tyngden G nedover og normalkraften N oppover fra kontaktflaten. Også normalkraften har en motkraft som virker nedover på underlaget. Legg merke til at normalkraften N fra underlaget er ikke en motkraft til G. Legg også merke til at den oppadrettede G-kraften ikke inngår i klossens kraftregnskap.

Ytre krefter og indre krefter

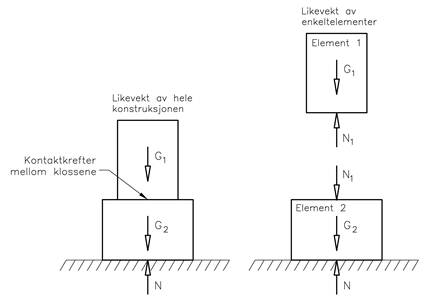
Figuren viser to klosser som ligger oppå hverandre. Hvis vi skal sette opp likevektslikninger for hele ”konstruksjonen” vil klossenes tyngde og kontaktkraften fra underlaget inngå i kraftregnskapet, dvs. N - G₁ - G₂ = 0. Mellom klossene finner vi kontakt­krefter som virker både på den øvre og den nedre klossen, men i og med at disse er like store og motsatt rettet (kraft = motkraft), vil disse nulle ut hverandre og således ikke gi noe bidrag i kraftregnskapet. Vi kaller slike krefter for indre krefter.

Hvis vi ser isolert på den øvre klossen så vil kontaktkraften N₁ inngå i kraftregnskapet, i og med at motkraften til N₁ ikke lenger er en del av kraftsystemet. N₁ har nå blitt en ytre kraft. Tilsvarende vil vi få for den nedre klossen. De enkelte bestanddeler til en konstruksjon kalles for konstruksjonens elementer. For en sammensatt konstruksjon kan vi alltid sette opp likevektsregnskap både på konstruksjonsnivå og på elementnivå.

Forbindelse mellom elementer

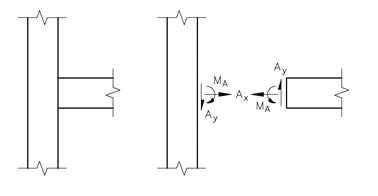
Konstruksjonselementene kan festes til hverandre og til omgivelsene på mange ulike måter, og som regel er vi nødt til å lage forenklede modeller av forbindelsene. Den faste forbindelsen som er vist under, overfører både en kraft og et kraftpar, og dette tilsvarer tre ukjente størrelser A_x, A_y og M_A.

Elementer kan også forbindes med såkalte bolteledd hvor det skjer en overføring av krefter mellom elementene, men ingen momentoverføring. Et slikt bolte­ledd kan betraktes som et felles boltelager for de to elementene, dvs. element 1 hviler på element 2 og vice versa.

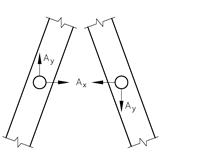
Det skjer en kraftoverføring i leddet som virker på begge elementene og denne leddkraften representerer to ukjente (størrelse og retning) som kan uttrykkes ved A_x og A_y.

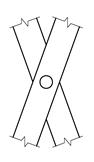
Strengt tatt utgjør også selve bolten et element slik det frem­kommer av figuren i midten, men i denne sammenheng er bolten uinteressant og vi ser bort fra denne. Figuren viser også hvilke krefter og motkrefter som hører sammen. Legg merke til at alle krefter går gjennom boltsenteret. Vi kommer tilbake til bolten i forbindelse med fagverkene.

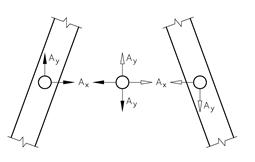
Kreftene som virker på de to elementene er like store og motsatt rettet og vi bruker betegnelsen A_x og A_y på begge elementene. Krefter og momenter som fremkommer når en konstruksjon splittes i to er krefter og motkrefter som er parvis like store og motsatt rettet, og derfor to sider av samme sak. Dette betyr at selv om vi får fire (alternativt seks) nye ytre krefter/kraftpar, så får vi bare to (alternativt tre) nye ukjente størrelser.

Reaksjonskrefter i forbindelsene

Vi skal nå se på hvordan vi kan bestemme reaksjonskrefter for sammensatte konstruksjoner. Oppgaven består i å bestemme alle reaksjonskrefter som virker på hvert element, dvs. både krefter i opplagringer og krefter gjennom elementforbindelsene. Vi oppsummer det vi har lært om de sammensatte konstruksjonene:

1. Elementene kan festes til hverandre med fast innspenning eller boltlager.
2. Vi kan sette opp likevektsuttrykk både på elementnivå og på konstruksjonsnivå
3. Hvis vi deler en konstruksjon i to må forbindelsen erstattes av nye ytre krefter i snittet som opptrer parvis
4. Snittkreftene virker på begge halvdelene og er motkrefter til hverandre, dvs. de er parvis like store men motsatt rettet.
5. Snittkreftene inngår i kraftregnskapet på for hver halvdel, men de inngår ikke i konstruksjonens kraftregnskap.

Figuren under viser en konstruksjon som deles opp i tre elementer. Den faste innspenningen erstattes med to krefter og et moment mens leddforbindelsen erstattes med to ukjente krefter.

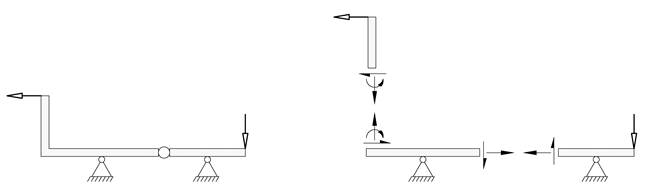
Når vi regner på sammensatte konstruksjoner kan det bli svært mange ukjente størrelser som skal bestemmes, og det blir viktig å arbeide systematisk og å tegne gode figurer. Det er spesielt viktig å holde oversikt over hvilke krefter som hører sammen og hvilke krefter som til enhver tid er bestemt og hvilke som gjenstår.

Elementtyper

En aksialstav er et rett element som bare er belastet med en kraft i hver ende og disse kreftene virker i stavens lengderetning. Pga likevekt må kreftene være like store og motsatt rettet. Aksiallasten N regnes vanligvis som positiv i strekk og negativ i trykk. Aksialstaver finner vi bl.a. i fagverk. Aksialstaven er en elementtype som har mange gode sider konstruksjons­messig og vi skal se nærmere på elementet senere. En bjelke er et element som er belastet med krefter som virker normalt på bjelkeaksen. En vertikal bjelke kalles gjerne en søyle.

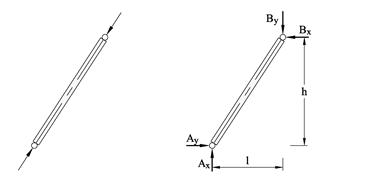
Et element som er leddet i hver ende og hvor all belastning skjer via leddene vil være en aksialstav. Det skyldes at det virker kun to krefter på elementet. Disse må være like store og motsatt rettet for å danne likevekt og eneste mulighet er da at kreftene virker i elementets akseretning. Dette er naturligvis en forenkling i og med at elementets egenvekt ikke virker i leddene, men i praksis vil egenvekten av aksialstaver være svært liten i forhold til de ytre lasten som virker på elementet. Vi kan også sette opp uttrykk som viser at kreftene i leddene virker langs elementaksen:

Symmetri

For en konstruksjon som er symmetrisk både med hensyn til geometri og belastning, vil også opplagerkrefter være symmetriske.

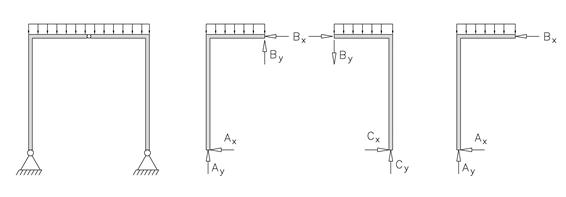
Symmetri gir oss at A_x = C_x, A_y = C_y og B_y = 0. Vi kan altså finne alle ukjente reaksjons­krefter ved bare å se på halve konstruksjonen.

Eksempler

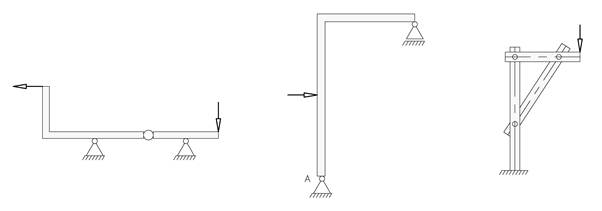
Det er tatt med tre regneeksempler på sammensatte konstruksjoner, et hvor elementene er fast innspent i hverandre og to eksempler hvor elementene er forbundet med bolteledd. Hvis ikke annet er oppgitt kan man anta at leddet ligger i bjelkenes akser, selv om noen figurer for oversiktens skyld tegnes med ledd som ikke ligger i aksen.