Et kraftpar er et kraftsystem av to like store og motsatt rettete krefter. Et kraftpar er en grunnstørrelse og kan derfor ikke reduseres til en kraftresultant. Mens en kraft har en translasjonsvirkning har et kraftpar en roterende virkning på legemet. Kraftparet kan oppleves som et litt abstrakt begrep, men husk på at hver gang du ser noe som roterer så er det et kraftpar som virker.

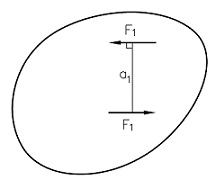
Kraftparet har tre karakteristiske kjennetegn; mål definert ved kraftparets dreiemoment (torque) T = Fa, dreieretning dvs. med eller mot klokka og orientering av kreftenes plan i rommet. I Meccanica begrenser vi oss til plane kraftsystem, og vi ser derfor bort fra kraftparets orientering. Kraftpar har benevningen Nm.

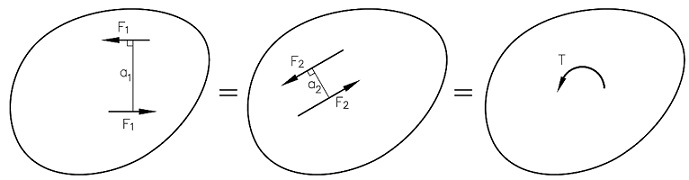
Kraftpar med samme dreiemoment og -retning har samme akselererende virkning i forhold til rotasjon og kalles derfor ekvivalente kraftpar. I kraftsystemene over er dreieretningen lik. Hvis dreiemomentene også er like, dvs. F₁a₁ = F₂a₂, er de to kraftparene ekvivalente. Legg merke til at kraftparets beliggenhet og angrepslinjenes retning er uten betydning. Et kraftpar kan dreies og flyttes omkring i planet uten at virkningen endres. Til og med kraftens mål kan velges vilkårlig så lenge armen tilpasses tilsvarende. Et kraftpar angis gjerne kun med et symbol som vist på figuren til høyre.Det kan virke pussig at man uten videre kan endre på kraftparet uten at virkningen endres. Men, hvis du skal løsne en bolt med et hjulkryss så spiller det liten rolle hvordan hjulkrysset er orientert eller hvor på hjulkrysset du holder.

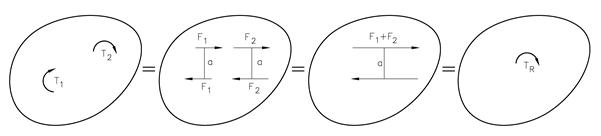
Figuren viser et legeme hvor det virker to kraftpar. Kraftparene kan dreies og flyttes fritt, og vi kan endre armen som vi selv vil, bare vi samtidig korrigerer kraftens mål. Dermed får vi følgende resultat:

T_R = (F₁ +F₂)a = F₁a + F₂a = T₁ + T₂

Kraftpar kan altså adderes algebraisk. Generelt får vi at T_R = ΣT_i. Også her må vi passe på fortegn, dvs. om kraftparet virker med eller mot klokka.

Flytting av angrepslinje

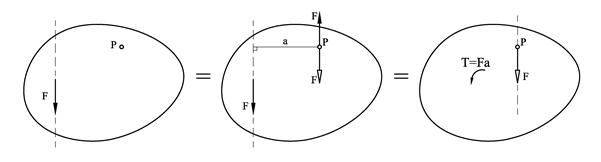
Vi ønsker å flytte kraften i figuren over slik at den angriper i punkt P. Men som vi har lært kan vi ikke uten videre flytte kraftens angrepslinje uten at virkningen endrer seg. Vi kan imidlertid plassere en ny kraft i P, med samme mål og retning som F hvis vi samtidig tar med en motkraft i P. Den opprinnelige kraften og den nye motkraften utgjør et kraftpar og vi står igjen med kraften F i P pluss et kraftpar med dreiemomentet T = Fa. Vi kan også gå motsatt vei. Ved å la F representere kraftparet kan kraftparet reduseres bort. Vær obs. på at et rent kraftpar ikke kan reduseres til en resultantkraft. En rotasjon kan aldri erstattes med en translasjon.

Resultantens beliggenhet

Vi skal nå se hvordan vi kan bestemme beliggenhet for resultanten av et vilkårlig kraftsystem.

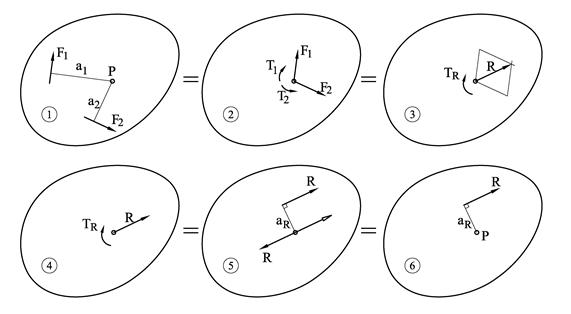
1. Figuren viser et legeme hvor det virker to krefter.
2. Alle krefter flyttes til punktet P og vi må legge til kraftpar med dreiemoment T₁ = F₁a₁ osv.
3. Med alle kreftene plassert i P kan kreftene vektoradderes og kraftparene summeres sammen.
4. Kraftsystemet er redusert til en resultantkraft og et resultantkraftpar.
5. Vi lar R representere kraftparet hvor a_R er bestemt av R·a_R = T_R
6. Kraftsystemet er redusert til en resultantkraft

Det er tatt med et eksempel som viser hvordan vi kan bestemme resultantens beliggenhet av parallelle krefter ved å flytte krefter sideveis.

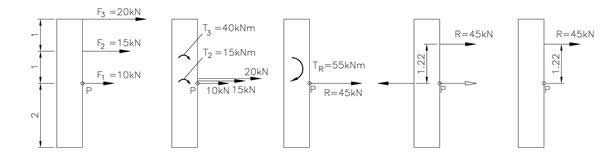
Vi kan flytte alle kreftene til P hvis vi samtidig legger til kraftpar;

T₂ =15·1=15kNm, T₃ = 20·2=40kNm, T_R = T₂ + T₃ = 55kNm

R = 10 + 15 + 20 = 45kN

R·a_R = T_R ⇒ a_R = 55/45 = 1,22m

I dette eksempelet hadde vi et system av parallelle krefter. Det er også mulig å bestemme resultanten av parallelle krefter grafisk, men dette er en nokså omstendelig metode som ikke bli behandlet her.

Vi har funnet fram til en metode for å bestemme resultantens beliggenhet. Metoden kan virke litt omstendelig, men legg merke til følgende; resultantens mål og retning bestemmes med vanlig vektoraddisjon, uansett hvor kreftene måtte være plassert. Videre ser vi at resultantens beliggenhet angitt med a_R bestemmes av uttrykket R·a_R = ΣF_i·a_i. Dvs. kraft ganger arm for resultanten er lik summen av kraft ganger arm for kraftsystemet. Dette er et et så viktig resultat at vi skal innføre begrepet kraftmoment hvor dropper alle mellomregninger og bruker resultatet R · a_R = ΣF_i · a_i direkte.