I mekanikken blir belastningene ofte fremstilt som en kraft som virker i et punkt, men punktlaster er egentlig en forenkling; alle belastninger har en viss utstrekning. Kontaktkrefter som virker på legemets overflate fordeler seg over et visst areal som trykk mens massekrefter som virker inni legemet, fordeler seg over et volum. Vi skal nå se nærmere på de fordelte lastene som f.eks. kan være snølaster, vindbelastning, hydrostatisk trykk, egenvekt osv.

Figuren under viser en bjelke som er belastet med en fordelt last som varierer langs bjelken og vi kan kalle den fordelte lasten for q(x). q(x) er en lastintensitet som angir kraft per lengdeenhet av bjelken. Vi bruker små bokstaver for fordelte laster (q i stedet for F) og enheten blir N/m.

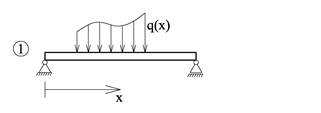
q(x) er gjerne en todimensjonal representasjon av et trykk p (N/m²) som virker over en flate og vi kan sette opp følgende sammenheng mellom lastintensitet og trykk: q = pb, hvor b er bredden som trykket virker over. 

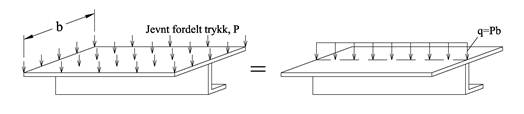
q kan også representere bjelkens egenvekt per løpemeter og vi får da følgende sammenheng mellom lastintensitet og materialets massetetthet: q = ρgA hvor A er tverrsnittsarealet.

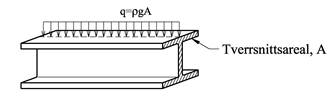
Når vi skal gjøre likevektsberegninger kan vi regne om den fordelte lasten til en resultantkraft som er en punktlast. Den fordelte lasten kan betraktes som en rekke parallelle krefter som virker over hvert sitt lille areal, og ved å summere disse opp får vi resultantkraftens mål. Generelt bestemmes R ved å summere opp q(x) over bjelkelengden, mens resultantens beliggenhet bestemmes vha momentteoremet:

             

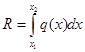
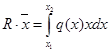
Legg merke til at resultanten er lik arealet under lastdiagrammet og at resultanten angriper i lastdiagrammets arealsenter. Som regel har vi ikke så kompliserte laster at det er behov for integrasjon og vi gjør i stedet enkle arealbetraktninger for å bestemme R og ­.

Figur (2) viser et lasttilfelle som kalles for en jevnt fordelt last hvor q har konstant verdi og vi får R = qL og . Figur (3) viser en jevnt voksende fordelt last med maksimumsverdi lik q hvor vi får og .

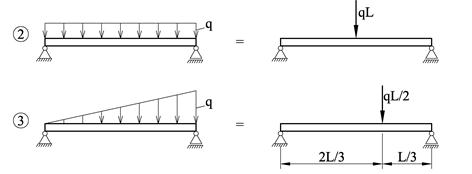
I de fleste tilfeller klarer vi oss fint med jevnt fordelte laster og jevnt stigende laster. Strengt tatt er det ikke nødvendig å gjøre de fordelte lastene om til en punktlast før man setter opp likevektslikningene. Vi skal også være obs på at når vi senere skal se på hva som skjer inni konstruksjonen (fasthetslæra) så blir det feil å erstatte fordelte laster med punktlaster.