Statisk likevekt er det mest sentrale begrepet i Meccanica, og statisk likevekt betyr kort og greit at legemet er i ro, eller har konstant hastighet. Man kan kanskje tro at statisk likevekt skyldes at det ikke virker noen kraft på legemet, men i praksis er alle legemer utsatt for krefters påvirkning på et eller annet vis. Vi får statisk likevekt når kraftsystemet som virker på legemet ikke har noen resultant. Og dette får vi typisk fordi legemet er fastholdt og forhindret fra å flytte på seg. Statisk liekvekt skriver vi gjerne som ΣF = 0.

Vi husker at resultanten av et kraftsystem kan bestemmes grafisk ved å legge kraftvektorene etter hverandre. Dersom vi lager et kraftpolygon av et kraftsystem i likevekt ender vi opp der hvor vi startet, dvs. vi får et lukket kraftpolygon.

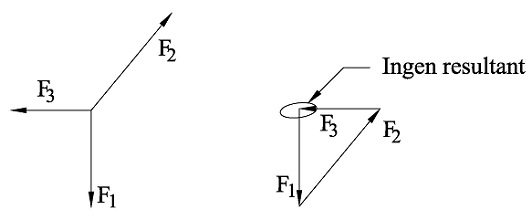
Frem til nå har problemstillingen vært å bestemme resultanten av et kraftsystem med kjente krefter. Men la oss si at vi belaster en konstruksjon med en eller annen kraft, og denne forblir i ro fordi den er holdt fast. Det skyldes at blir I statikk er problemstillingen typisk en annen; konstruksjonen er i ro og vi har ingen resultant, men noen av kreftene som inngår i kraftsystemet er ukjent og vi skal bestemme disse. Vi stiller spørsmål av typen hvor stor må kraft nr. 2 være for at resultanten skal være null osv.? Vi sier at vi løser likevektslikninger. Typisk har vi en situasjon hvor konstruksjonen utsettes for ytre belastninger med kjente størrelser. Konstruksjonen forblir den i ro pga reaksjonskrefter som motvirker belastningen. Til sammen danner den ytre belastningen og reaksjonskreftene en kraftlikevekt. Oppgaven i statikk består altså i å bestemme ukjente reaksjonskrefter som følge av ytre belastninger. Dette gjør vi ved å løse såkalte likevektslikninger.

Vi skal bestemme ukjente krefter som inngår i et kraftsystem i likevekt og de ukjente størrelsene kan være krefters mål, retning eller beliggenhet. Dreiemoment kan også være en ukjent størrelse.

Likevekt av to krefter

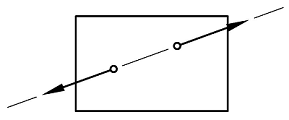
Hvis et kraftsystem i statisk likevekt består av kun to krefter så må de to kreftene være like store, motsatt rettet og ligge på samme angrepslinje. Vær obs på spesialtilfellet kraftpar hvor de to kreftene er like store, motsatt rettet, men ikke ligger på samme linje. Dette gir en rotasjon og vi har derfor ikke statisk likevekt.

Likevekt av tre krefter

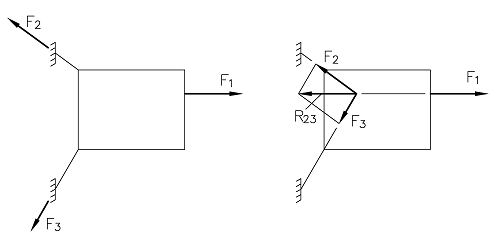
Figuren viser et kraftsystem av tre krefter som er i statisk likevekt. Resultanten av F₂ og F₃ kan vi kalle R₂₃. Da må R₂₃ og F₁ være like store, motsatt rettet og ligge på samme angrepslinje. R₂₃ angriper i skjæringspunktet mellom F₂ og F₃. Det gjør også F₁ (ellers får vi et kraftpar). Tre krefter som danner likevekt må derfor være sammenløpende. På tilsvarende vis kan vi vise at R₁₂ er like stor, motsatt rettet og ligger på samme angrepslinje som F₃ osv.

Legg merke til følgende spesialtilfelle; hvis to av tre krefter i likevekt ligger på samme angrepslinje så ligger alle tre kreftene på samme angrepslinje.

Likevekt av fire krefter

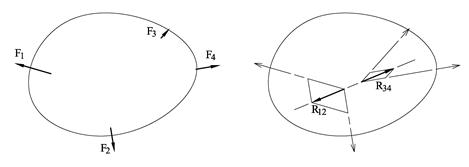
Her vil resultanten R₁₂ av F₁ og F₂ er like stor, motsatt rettet og ligger på samme angrepslinje som R₃₄. Tilsvarende forhold vil vi ha mellom R₁₃ og R₂₄ osv.

Grafisk metode for å bestemme ukjente krefter

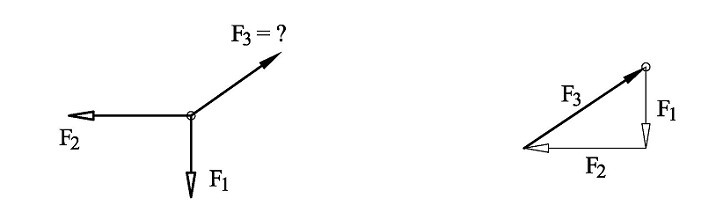
Vi skal nå se på hvordan vi grafisk kan bestemme ukjente krefter som inngår i et kraftsystem som er i likevekt. Figuren under viser et kraftsystem i likevekt hvor kraften F₃ har ukjent mål og retning. Vi tegner en hjelpefigur hvor vi legger F₁ og F₂ etter hverandre. F₃ lukker polygonet.

I figuren under har vi to krefter med ukjent mål, men retningen er kjent. Vi tegner en hjelpefigur og begynner med den kjente F₁. Deretter tegner vi to linjer med retninger i samsvar med F₂ og F₃. Linjene skjærer hverandre og vi har fått et lukket polygon.

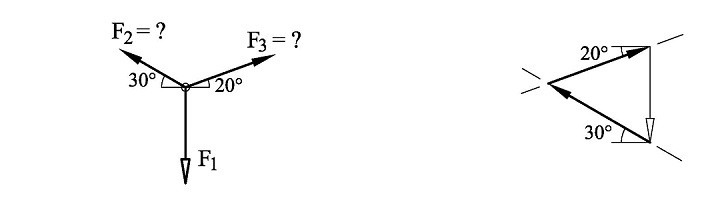
Analytisk metode for å bestemme ukjente krefter

Å bestemme ukjente krefter grafisk kan være nokså omstendelig og vi skal nå se hvordan vi kan regne oss fram til ukjente krefter som inngår i et likevektssystem.

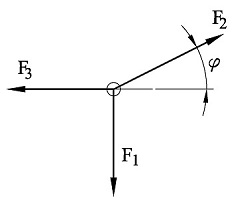
Figuren over viser en liten ring som er belastet med tre krefter som til sammen danner likevekt, og de tre kreftene er sammenløpende. Likevekt betyr at kraftsystemet ikke har noen resultant, som igjen betyr at vi summen av krefter i både x- og y-retning er lik null. Vi kan f.eks. skrive R_x = F_2x - F₃ = 0 og R_y = F_2y - F₁ = 0. Legg merke til at vi har bare to likninger; hvis f.eks. F₁ og F₃ er kjent kan vi regne oss fram til F_2x og F_2y og dermed er F₂ bestemt.

Likevekt betyr at kreftene skal være i "balanse", og det er mange måter å uttrykke dette på. Vi kan f.eks. si at det skal være like mye kraft som virker oppover og nedover og like mye som virker mot høyre og mot venstre. En annen måte å sette opp et "likevektsregnskap" på kan være at de ukjente kreftene skal være like store som de kjente kreftene:

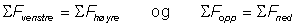
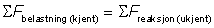
I Meccanica skal vi bruke følgende oppsett for likevektslikninger. Vi begynner med å velge en positiv x- og y-retning. Her står vi fritt, det eneste kravet er at retningene er vinkelrett i forhold til hverandre. Den positive retningen angis ved å tegne en pil foran likevektsuttrykket. Vi får to likevektsuttrykk hvor vi summerer vi opp henholdsvis x- og y-komponenetene og summen skal være lik null. Vi skriver:

Det er en forutsetning at vi bruker fortegn på komponentene, og kraftkomponenter som virker motsatt vei i forhold til den positive retningen får minus. I Meccanica velger vi gjerne x-retning ”mot venstre” og y-retning ”oppover” med mindre det er regnemessige fordeler å velge andre retninger (f.eks. for å unngå mange minus'er i likningene). Av og til vil vi også velge "skråstilt" x-og y-retning. For kraftsystemet over kan vi sette opp følgende likevektsuttrykk:

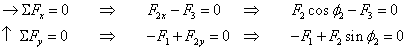
I mekanikk står løsing av likevektslikninger svært sentralt. For sammenløpende kraftsystemer kan vi sette opp kun to likevektslikninger, og det betyr at vi f.eks. kan bestemme F_2x og F_2y og dermed er både mål og retning for F₂ bestemt. Alternativ kunne vi bestemt målet til F₁ og F₃ dersom F₂ var kjent.

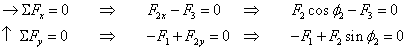
Trigonometri er et viktig hjelpemiddel i mekanikk. Bl.a. må vi dekomponere krefter som ikke sammenfaller med x- og y-retningen når vi setter opp likevektslikningene. Så om du er litt ”rusten” i trigonometri så er det på tide å friske opp denne kunnskapen nå. Figuren under oppsummerer det du trenger å vite, lengden A er den kjente størrelsen.

Det er helt avgjørende at man tegner en figur som viser retning og plassering for alle krefter, både de kjente og de ukjente. En slik figur kalles ”fritt-legeme-diagram” og alle likevektsberegninger begynner med dette diagrammet.