Vi har lært en del om statisk likevekt men fram til nå har vi begrenset oss til systemer av sammenløpende krefter. Vi skal nå gå videre og se på likevektslikningene for ethvert plant kraftsystem. Et kraftsystem er i likevekt hvis kraftsystemet oppfyller følgende 3 likevektslikninger:
ΣFx = 0 for enhver akseretning
ΣFy = 0 for enhver akseretning
ΣMp = 0 for ethvert momentpunkt
De to første betingelsene sikrer at resultanten ikke kan være en kraft, og den siste betingelsen utelukker at resultanten kan være et kraftpar. Både ΣFx = 0 og ΣFy = 0 kan erstattes med en momentlikning. Så lenge punktene A, B og C ikke ligger på linje kan vi f.eks. bruke ΣMA = 0, ΣMB = 0 og ΣMC = 0 som betingelser for statisk likevekt. Figuren under illustrerer prinsippet:

ΣMA = 0 og ΣMB = 0 innebærer at resultantens angrepslinje må gå gjennom hhv. punkt A og punkt B. Eneste mulighet er dermed at resultanten ligger på linjen AB. SMC = 0 (forutsatt at ABC ikke er på linje) betyr at vi ikke kan ha noen resultant. Generelt kan vi sette opp tre alternative sett med likevektslikninger:
|
Alt. 1 ΣFx = 0 ΣFy = 0 ΣMp = 0 |
Alt. 2 ΣFx = 0 ΣMA = 0 ΣMB = 0 AB ikke parallell med y |
Alt. 3 ΣMA = 0 ΣMB = 0 ΣMC = 0 ABC ikke på linje |
Setter vi opp flere likevektslikninger for legemet vil vi oppdage at det bare er tre som er uavhengige. De øvrige likevektsikningene representerer kombinasjoner av de tre første. Vi har aldri mer enn tre likevektslikninger for et legeme, og vi er i stand til å bestemme kun tre ukjente størrelser ved hjelp av statikkens lover. Vi kan bare sette opp tre likevektslikninger, men vi har stor grad av frihet i forhold til hvilke likninger vi vil bruke. Og det vil kreve litt trening for å kunne se hvilke likninger det "lønner" seg å sette opp. vi velger først hvilken ukjent størrelse som skal bestemmes, deretter setter opp den likevektslikningen som passer best for formålet. Så langt det lar seg gjøre forsøker vi å sette opp likevektslikninger som gir bare en ukjent størrelse per likning, og derfor tar vi ΣFy – likningen til slutt i eksemplet over. Tilsvarende må vi velge momentpunkt med omhu når vi setter opp momentlikninger slik at kun en ukjent størrelse inngår. Vi velger typisk momentpunkter som ligger på angrepslinjen til ukjente krefter, hvorfor det? Oppsett og løsing av likevektslikninger er svært sentralt i mekanikk, og dette inngår som en del av nesten alle oppgaver. Det er derfor viktig å regne mange oppgaver slik at metodikken sitter godt.
Uavhengighetsprinsippet
I statikk antar vi at deformasjonene som følge av belastningene er så små at ikke geometrien endres, dvs. at kreftenes retning og momentarmer ikke påvirkes. Dette medfører at man kan bestemme virkningen (reaksjonskrefter, nedbøyning osv) av den enkelte last hver for seg. Virkningen av det totale lastsystem blir da summen av delvirkningene. Figuren under illustrerer prinsippet (kalles også superposisjonsprinsippet)
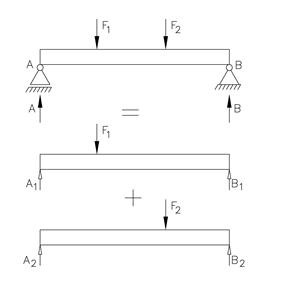
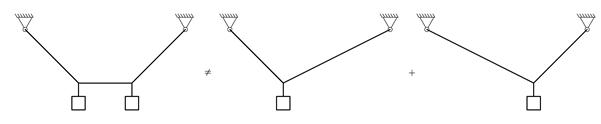
For eksemplet over får vi A = A1 + A2 og B = B1 + B2. For systemer hvor geometrien i vesentlig grad påvirkes av kreftene som virker på systemet kan uavhengighetsprinsippet ikke anvendes.
Reaksjonskrefter
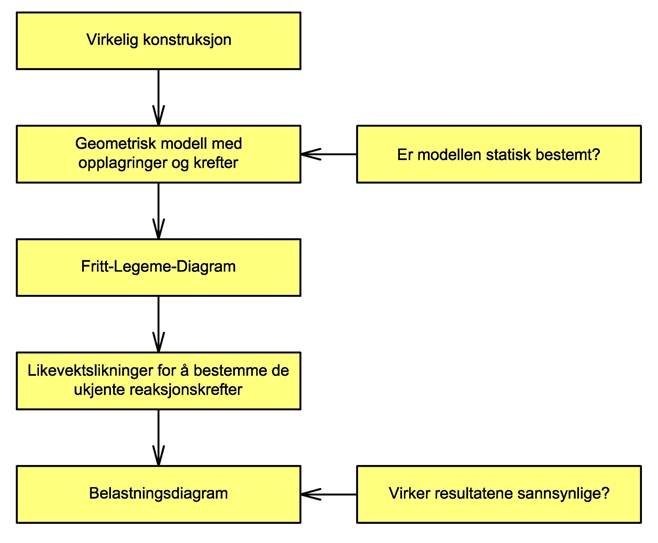
Bestemmelse av reaksjonskrefter inngår i de fleste oppgaver i statikk. Disse kalles gjerne fastholdningskrefter eller opplagerkrefter. Vi skal her presentere en generell prosedyre som vi kan bruke for å bestemme de ukjente reaksjonskrefter. Vi skal stort sett følge denne prosedyren, men av og til blir prosedyren unødvendig omstendelig og vi kan da ta noen snarveier.
Formålet med å bestemme reaksjonskreftene er at vi vil ha full oversikt over alle krefter som virker på konstruksjonen før vi går videre og løser vårt mekanikkproblem. Vi skal nå illustrere metodikken med eksempelet under hvor vi skal gjøre beregninger på en såkalt løpekattbjelke.

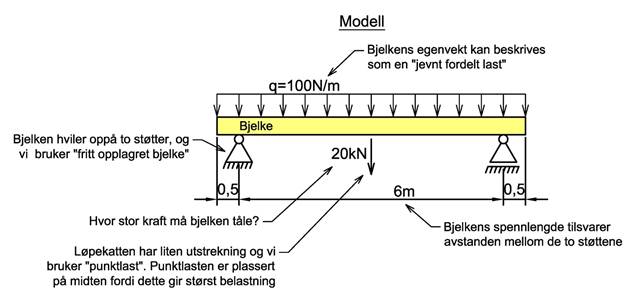
Mekanikk handler om virkelige konstruksjoner, men for at beregningene ikke skal bli alt for kompliserte må vi gjøre noen antakelser og forenklinger. Vi lager en modell av konstruksjonen som inneholder den informasjon vi behøver for å kunne gjøre våre beregninger. Modellen må beskrive den geometriske utformingen av konstruksjonen og den må beskrive kreftene som virker på konstruksjonen. Hvilke dimensjoner har konstruksjonen? Hva skal tas med i modellen? Vi kan ikke ta med alle detaljer og vi må avgrense modellens utstrekning. Der modellen stopper, må vi velge opplaginger som sier noe om hvordan konstruksjonen forholder seg til omgivelsene. Vi må vite hvor store krefter som virker på konstruksjonen, hvordan kreftene fordeler seg (skal vi bruke punktlast eller jevnt fordelt last), hvor kreftene virker og hvilken retning de har. Er det flere krefter på konstruksjonen og virker disse samtidig? Må vi ta hensyn til konstruksjonens egenvekt? De ytre kreftene kan variere mye og vi baserer gjerne våre beregninger på de største tenkelige kreftene og med den ugunstigste plasseringen, slik at vi er på den sikre siden. Å lage en modell som beskriver den virkelige konstruksjonen på en tilfredsstillende måte kan være vanskelig og krever gjerne en del erfaring. Figuren under viser en modell av bjelken som er vist på bildet over.
Vi kontrollerer om modellen er statisk bestemt modell slik at vi kan løse problemet ved hjelp av likevektslikningene. Vi tegner et fritt-legeme-diagram hvor alle opplagringer erstattes med ukjente reaksjonskrefter. Vi velger et koordinatsystem og reaksjonskreftene gis navn, f.eks. Ax, Ay og MA. Sammensatte konstruksjoner deles opp ved ledd og ved stive forbindelser.
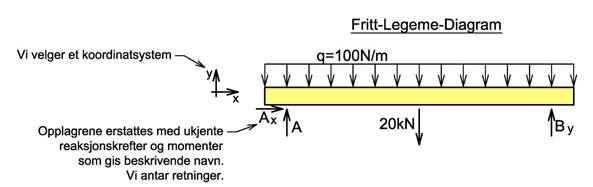
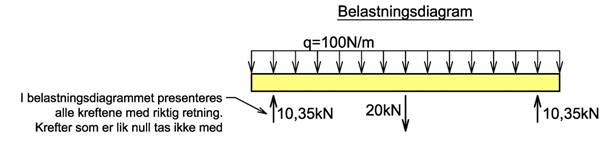
Vi bruker likevektslikningene for å bestemme de ukjente reaksjonskreftene og presenterer våre beregninger i et belastningsdiagram. I belastningsdiagram tegnes både de ytre kreftene og reaksjonskreftene, og kreftene tegnes med riktig retning og krefter som er lik null tas ikke med. Til slutt ser vi over resultatene og vurderer om beregningene virker sannsynlige. Er det like mye kraft som virker oppover som nedover osv? Belastningsdiagrammet danner utgangspunkt for de videre beregningene.
Opplagring
For at en konstruksjon som er utsatt for belastning skal forbli i ro, må den være fastholdt på et eller annet vis. En konstruksjon kan fastholdes på mange forskjellige måter og vi innfører symboler som representerer ulike opplagerbetingelser.
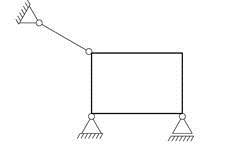
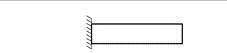
Kraftoverføring:
Stanglager (tau): I stangens retning (1 ukjent)
Glidelager: Normalt på planet (1 ukjent)
Boltlager: I alle retninger (2 ukjente)
Fast innspenning: I alle retninger pluss kraftpar (3 ukjente)
Formålet med opplagerbetingelsene er å beskrive hvordan legemet er forbundet med omgivelsene. Den virkelige forbindelsen er neppe 100% slik som opplagerbetingelsene angir. Opplagrene må betraktes som en idealisering, og det vil ofte være nødvendig å gjøre en grundig ingeniørvurdering av den virkelige konstruksjonen for å velge rett opplagerbetingelse. Mange innfestninger ligger nok et sted mellom fast innspenning og boltelager. Når en konstruksjon belastes med ytre krefter så oppstår det reaksjonskrefter i opplagene eller innfestningen og det er disse som skaper likevekt. Opplagrene er en måte å beskrive hvordan konstruksjonen forholder seg til omgivelsene. Valg av opplagre kan ha stor betydning for beregningsresultatet men vi skal ikke gå inn i dette temaet.
Fritt-Legeme-Diagram
Statikk handler typisk om å bestemme reaksjonskrefter der hvor konstrukjonen er fastholdt, som følge av de ytre belastningene som virker på konstruksjonen. Vi starter alle oppgaver med å skaffe oss en oversikt over kreftene som virker på legemet, både kjente og ukjente, og en slik oversikt får vi ved å tegne et såkalt fritt-legeme-diagram (FLD) hvor alle opplagrene erstattes med ukjente reaksjonskrefter. Formålet med FLD er å få fram alle krefter som virker på legemet, hvor disse er plassert og kreftenes retning. Først da har vi grunnlag for å sette opp likevektslikninger.
Modell Fritt-Legeme-Diagram
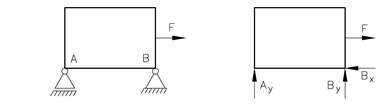
Glidelageret erstattes med Ay mens boltlageret hvor både mål og retning er ukjente størrelser, erstattes med Bx og By
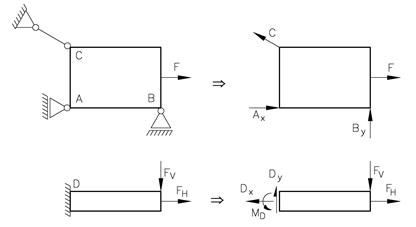
Glidelagrene erstattes med Ay og By mens stanglageret erstattes med C. Den faste innspenningen kan overføre både kraft og moment, og erstattes med de tre ukjente størrelsene Dx, Dy og MD. De ukjente opplagerkreftene navngis som Ax, By osv. En alternativ skrivemåte kan være FAx og FBy. I D virker det et kraftpar som vi benevner MD. Uten momentet i D ville konstruksjonen ikke være i stand til å bære lasten. I FLD er det ukjente størrelser og her må vi anta en kraftretning. Selv om vi formelt sett ikke kjenner kraftretningen gjør vi gjerne en vurdering av konstruksjonen og lastbildet når vi setter opp et FLD, og vi forsøker så langt det er mulig å velge rett kraftretning. Regnemessig er det en viss fordel om vi antar riktig retning. Når FLD er satt opp har vi et fint utgangspunkt for å bestemme de ukjente størrelsene ved hjelp av likevektslikningene. Vi kan sette opp likevektslikninger på mange forskjellige måter; vi velger først hvilken ukjent størrelse som skal bestemmes, deretter setter opp den likevektslikningen som passer best for formålet. Så langt det lar seg gjøre forsøker vi å sette opp likevektslikninger som gir bare en ukjent størrelse per likning, og derfor tar vi ΣFy – likningen til slutt i eksemplet over. Tilsvarende må vi velge momentpunkt med omhu når vi setter opp momentlikninger slik at kun en ukjent størrelse inngår. Vi velger typisk momentpunkter som ligger på angrepslinjen til ukjente krefter, hvorfor det?
Belastningsdiagram
Når de ukjente opplagerkreftene er bestemt presenterer vi resultatene i et såkalt belastningsdiagram (BD) som viser samtlige krefter som virker på konstruksjonen. BD er temmelig likt FLD, men det er satt inn verdier for de ukjente størrelsene. Vær obs. på at krefter som er lik null ikke skal tas med og at alle krefter skal tegnes med rett kraftretning. Dersom man regner seg fram til en negativ kraft så skal pilen alltid snus. BD gir det totale bildet av belastningene på konstruksjonen og man bør alltid gjøre en vurdering av om resultatene i belastningsdiagrammet virker troverdige. Likevektslikningene kan betraktes som et kraftregnskap, dvs. at det skal virke like mye krefter oppover som nedover og like mye krefter mot høyre som mot venstre. Vi avslutter gjerne oppgaven med å sjekke kraftregnskapet.
