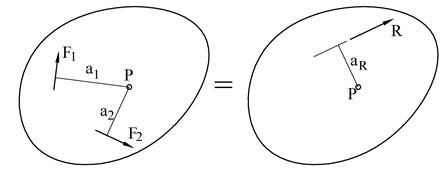Kraftmomentet, eller bare momentet, er et sentralt begrep i mekanikk. Momentet er et regnemessig hjelpemiddel som ikke har noen fysisk betydning, men som vi bruker f.eks. når vi beregner resultantens beliggenhet. Kraftmomentet har mange paralleller til kraftparet og det er ikke uvanlig at disse begrepene brukes om hverandre.

Kraften F sitt moment om punktet P er definert som P M_p = F·a, hvor kraftens arm a er avstanden fra P normalt ned på kraftens angrepslinje. P er momentets dreieretning. Kraftmomentet har enheten Nm. Momentpunktet P er et fritt valgt referansepunkt som kan ligge i eller utenfor legemet, men det må ligge i samme plan som kraftsystemet.

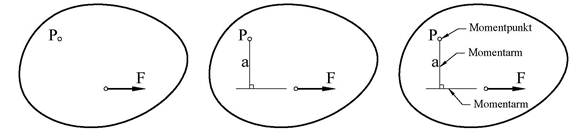
Slik momentbegrepet er definert vil momentets mål være avhengig av momentpunktets beliggenhet, og vi må derfor alltid angi momentpunktet. Momentet om punkt A angis som M_A osv.

 

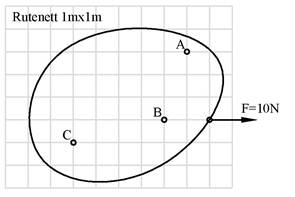
PM_A = -30Nm

M_B = 0Nm

PM_C = 10Nm

 

 

Med dreieretning mener vi kraftens dreieretning i forhold til momentpunktet, og det betyr at også dreieretningen vil kunne endre seg avhengig av momentpunktets beliggenhet i forhold til kraften F. Man kan forestille seg at legemet holdes fast i momentpunktet og spørre seg; vil kraften føre til at legemet roterer med eller mot klokka? I tilfellet over virker M_A "mot klokka" mens M_C virker "med klokka". I stedet for å skrive "med klokka" eller "mot klokka" definerer vi en positiv dreieretning med symbolene P og Q og lar fortegn angi den faktiske dreieretningen. I eksemplet over kan både skrive PM_A = -30Nm og QM_A = +30Nm. Legg merke til at om vi flytter en kraft langs sin angrepslinje så blir momentet uendret:

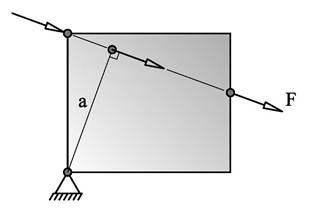
Vi kan beregne momentet på to alternative måter. I figuren under er vist en situasjon hvor vi kjenner avstanden d mellom momentpunktet P og kraftens angrepspunkt. Vi kan enten beregne momentarmen a = d·cosϕ eller vi kan beregne kraftkomponenten F_^ = F·cosϕ og bruke d som momentarm.

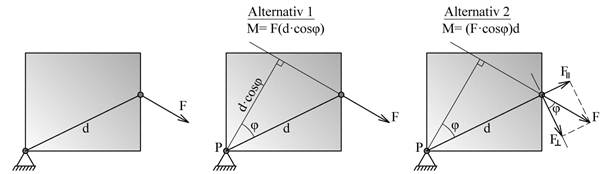
Momentteoremet

Figuren viser et legeme hvor det virker to vilkårlige krefter F₁ og F₂. Resultanten R til de to kreftene er også vist, jf. parallellogramloven. Vi kan finne momentet for F₁, F₂, og R ved å dekomponere disse ned på en linje som ligger normalt på d. Vi ser av figuren at R_^ = F_1^ + F_2^a. I om med at momentarmen d er den samme for F₁, F₂, og R får vi at d·R_^ = d·F_1^ + d·F_2^.

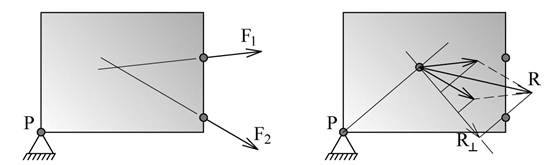
Vi kan derfor slå fast at resultantens moment om et vilkårlig punkt P er lik summen av enkeltkreftenes momenter om P. Vi setter opp momentteoremet som er en svært viktig læresetning i mekanikk.

Resultantens moment om et vilkårlig punkt P er lik summen av enkeltkreftenes momenter om P R · aR = ΣMPi = Σ(Fi · ai)

Momentteoremet kan bl.a. brukes for å bestemme resultantens beliggenhet. Vi ser at momentene skal adderes sammen direkte, forutsatt at kraftsystemet er plant. Når vi skal summere momentene må vi passe på fortegn. I tilfellet under får vi f.eks. ΣM_P = F₁a₁- F₂a₂ dersom P er positiv dreieretning. Dersom ΣM_P er større enn null så skal R gi samme dreieretning.