Vi kan oppnå den samme akselerasjonen for et legeme ved å påføre krefter på mange forskjellige måter, og vi sier at alle kraftsystemer som resulterer i den samme akselerasjonen er likeverdige eller ekvivalente. Om vi erstatter det virkelige kraftsystemet med et annet ekvivalent kraftsystem, så blir virkningen den samme. Det er mulig å erstatte ethvert kraftsystem med kun en enkelt kraft. Husk på at det er ikke den enkelte kraft men summen av alle kreftene som gir akselerasjon, og selv et komplisert kraftsystem gir bare en enkel akselerasjon. Vi kaller en slik ekvivalent enkeltkraft for kraftsystemets "resultant". Resultanten er en fiktiv kraft med samme retning og beliggenhet som akselerasjonen og med målet F = ma. Vi bruker bokstaven R som navn på resultanten.

Figuren under viser en vogn hvor det virker to krefter F₁ og F₂. Vogna får en akselerasjon mot høyre som om det virket en kraft på 2kN mot høyre. For krefter som virker langs samme linje kan kreftene adderes direkte for å finne resultanten.

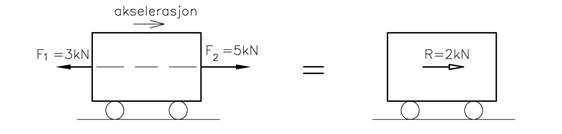
I figuren under er F₁ og F₂ like store. Vi får ingen akselerasjon og følgelig er det heller ingen resultantkraft. Vi sier at kraftsystemet er i statisk likevekt.

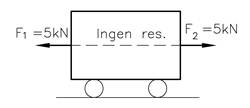
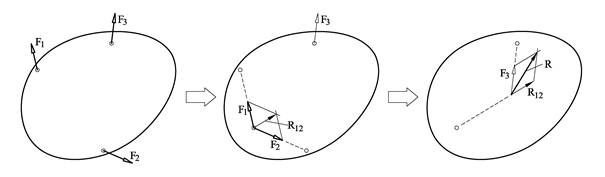
Figuren under viser en kloss med to krefter som angriper i hver sin retning. Kreftene resulterer i en akselerasjon med retning som vist på figuren. Ved å gjøre målinger av akselerasjonen kan vi beregne resultantens mål og retning.

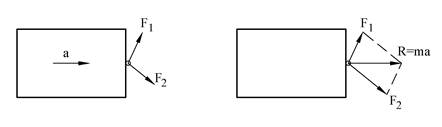
Det viser seg å være en geometrisk sammenheng mellom F₁, F₂, og R. Vi setter opp parallellogramloven:

Dette er en grunnleggende naturlov som kan vises med forsøk, men den kan ikke bevises. Sammenhengen kan matematisk uttrykkes som en vektoraddisjon. I Meccanica finner du flere eksempler på hvordan vi bestemmer resultanten grafisk. I noen eksempler benytter vi oss av muligheten vi har til å flytte krefter langs angrepslinjen når vi skal bestemme resultanten.

Resultanten av kraftsystem med flere sammenløpende krefter

Figuren viser et kraftsystem med flere krefter og kreftenes mål og retning er angitt med et rutenett. Vi skal bestemme kraftsystemets resultant.

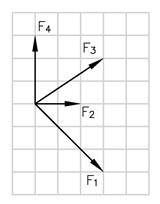
Resultanten R₁₂ av F₁ og F₂ kan bestemmes ved å legge F₁ og F₂ etter hverandre. Deretter kan R₁₂₃ bestemmes ved å legge R₁₂ og F₃ etter hverandre osv.

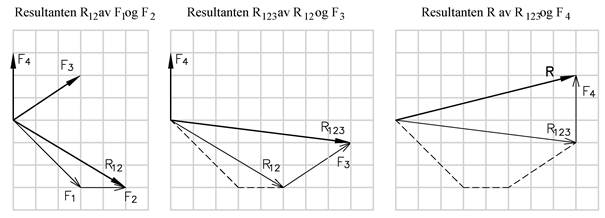
Vi ser at resultanten kan bestemmes ved å legge alle kraftpilene etter hverandre. Vi kaller dette for et kraftpolygon, og resultanten finner vi som vektoren fra startpunktet til sluttpunktet i kraftpolygonet. Vi kan lage mange forskjellige kraftpolygoner ved å legge sammen kreftene i forskjellig rekkefølge, men vi vil uansett ende samme sted. Kreftenes rekkefølge i kraftpolygonet er altså likegyldig. I og med at kreftene er sammenløpende går resultantkraften gjennom det felles skjæringspunktet.

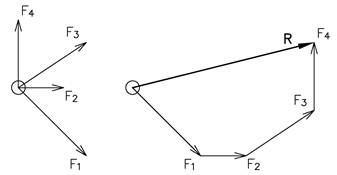
Resultanten av et generelt plant kraftsystem

Figuren viser et plant kraftsystem hvor kreftene ikke er sammenløpende. I slike tilfeller bygges resultanten gradvis opp ved å legge til en og en kraft, dvs. først R₁₂ = F₁ + F₂, deretter R₁₂₃ = R₁₂ + F₃ osv.

Retning og mål finner vi på vanlig vis med vektoraddisjon av alle krefter, uansett hvor disse måtte befinne seg. Vi kan derfor sette opp følgende generelle regel:

Legg merke til at det kan være nokså omstendelig å bestemme resultantens beliggenhet grafisk, når kreftene ikke er sammenløpende. Det er langt enklere å bestemme beliggenheten med regning. Parallelle krefter som vi f.eks. har ved tyngdepunktsberegninger er et eksempel på kraftsystem som er vanskelig å løse ved den grafiske metoden.

Dekomponering

Vi har sett hvordan vi komponerer resultanten ut fra to kraftkomponenter. På tilsvarende vis kan vi dekomponere en kraft i to komponenter, dvs. vi kan gå andre veien.

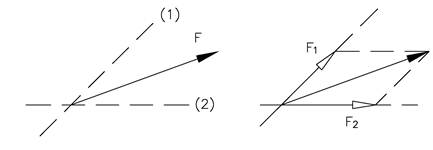
Hvis vi dekomponerer i to ortogonale retninger får vi følgende komponenter:

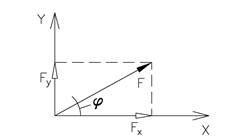
Dette er et spesialtilfelle som vi skal benytte oss av når vi skal bestemme resultanten med regning.

Resultanten bestemt med regning

Vi har sett hvordan vi kan bestemme resultanten av et kraftsystem ved hjelp av en tegning. Den grafiske metoden er svært nyttig fordi den gir en god forståelse av kraftbildet, men den har sine begrensinger når kraftsystemet blir komplisert. Vi skal her se på den analytiske metoden hvor vi bestemmer resultanten ved hjelp av regning.

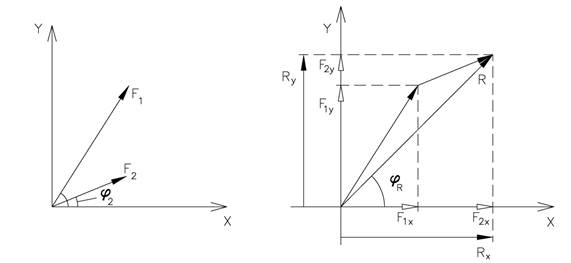
Figuren over viser to krefter F₁ og F₂ som er lagt inn i et koordinatsystem. I høyre figur er kreftene dekomponert i x- og y-retningen. Legg merke til at resultantens x-komponent er lik summen av kreftenes x-komponenter, dvs. R_x = F_1x + F_2x. Tilsvarende får vi i y-retningen. Den analytiske metoden for å bestemme resultantens mål og retning går som følger; vi velger et koordinatsystem og hver kraft dekomponeres i x- og y-retningen. Komponentene adderes sammen og vi får R_x og R_y. Resultantens mål bestemmes med pytagoras mens retningen bestemmes ved trigonometri. Vi kan sette opp følgende uttrykk for resultanten av to krefter:

I og med at komponentene ikke nødvendigvis "peker samme vei" må vi passe på fortegn når vi adderer sammen x- og y-komponentene. Vi må derfor først angi positive akseretninger, og komponentenes fortegn bestemmes av om komponenten er rettet med eller mot den positive akseretningen.

Resultanten av mange krefter bestemmes i prinsippet på samme måte som vist over, men vi får da flere ledd som inngår i R_x og R_y.

For å bestemme resultantens beliggenhet bruker vi momentteoremet som sier at resultantens moment om et fritt valgt referansepunkt P er lik summen av enkeltkreftenes momenter om P, dvs. Ra_R=Σ(F_ia_i).

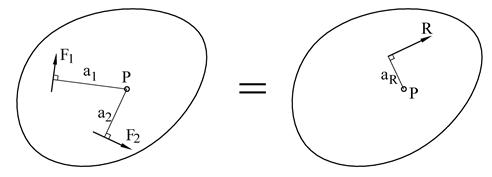
Det er viktig å tegne en god figur som viser kreftenes retning og beliggenhet, men når vi arbeider analytisk blir kravet til figurens nøyaktighet naturligvis ikke det samme som når vi jobber grafisk.