Fram til nå har vi konsentrert oss om å bestemme reaksjonskrefter i opplagrene. Det neste skrittet er å kartlegge hvilke krefter og momenter som virker inni konstruksjonen. Det er nødvendig å kjenne de indre kreftene når vi etter hvert skal undersøke om materialet tåler belastningen eller om konstruksjonen bryter sammen.

Figuren viser en fritt opplagret bjelke som er belastet med diverse krefter. La oss tenke oss at denne bjelken består av to halvdeler som er festet til hverandre. Hver halvdel skal også være i likevekt og det betyr at det må virke krefter på snittflaten, og det er disse snittkreftene som holder de to delene sammen. Vi kan bestemme snittkreftene ut fra likevektskrav til bjelkehalvdelene. Generelt vil vi ha følgende snittkrefter; en normalkrat N som virker i bjelkens akseretning, en skjærkraft V som virker på tvers av bjelkeaksen og et bøyemoment M som virker i belastningens plan.

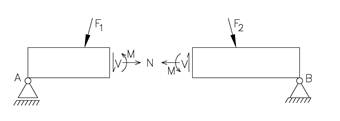
Snittkreftene er indre krefter som opptrer parvis som krefter og motkrefter på hver sin side av tverrsnittet. I og med at kraft og motkraft virker hver sin vei, blir fortegnsreglene litt kompliserte. Figuren under viser positiv retning for henholdsvis N, V og M.

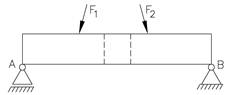
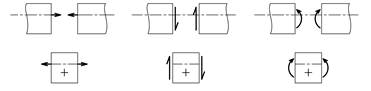
Normalkraften N er positiv når den gir strekk i bjelken.

Skjærkraften V er positiv når den roterer elementet med klokken.

Bøyemomentet M er positivt når bjelken får strekk på bjelkens underside.

Fortegnsregelen for bøyemomentet er noe ufullstendig i og med at den forutsetter at vi vet hva som er undersiden.

Det er snittkreftene som gir en belastning på bjelkematerialet og vi er derfor interessert i å finne de største snittkreftene i bjelken. Snittkreftene varierer langs bjelken og vi skal lære hvordan vi kan lage momentdiagram, skjærkraftdiagram og normalkraftdiagram som gir en god oversikt over snittkreftene.

Sammenheng mellom V- og M-diagram

For en rett bjelke med fordelt belastning q(x) er de tre funksjonene V(x), M(x) og q(x) knyttet sammen på følgende vis:

Tverrlasten er altså den deriverte av skjærkraften, som igjen er den deriverte av bøyemomentet, og dette kan vi bruke til å finne topp- og bunnpunkt i momentdiagrammet. Vi kan også finne momentet vha arealet under skjærkraftdiagrammet. Generelt har vi:

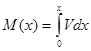
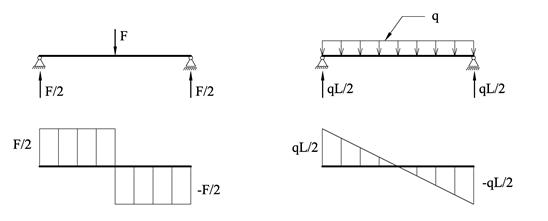
Vi skal se hvordan vi kan bruke arealer under skjærkraftdiagrammet for å finne det dimensjonerende bøyemoment for to viktige lasttilfeller.