Figuren viser en kloss som står i ro på et flatt underlag. Hvis vi påfører en kraft på tvers, er det to ting som kan skje; klossen glir og det betyr at vi har et friksjonsproblem eller klossen velter og da har vi et stabilitetsproblem.

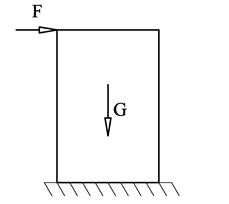
Dette er en spesiell type problem som handler om å kontrollere en belastning i forhold til en grenseverdi hvor legemet går fra en tilstand til en annen. Her gjør vi altså ikke likevektsbetraktninger. Typiske spørsmål kan være; "hvor stor kraft kan vi ha før klossen velter" og "hva er sikkerhetsfaktoren i forhold til glidning?"

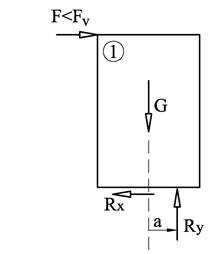
I situasjonen over er det påført en ytre kraft F som er mindre enn veltekraften og klossen forblir i ro. Klossen holdes i likevekt av en friksjonskraft fra underlaget R_x, og til sammen danner F og R_x et kraftpar med momentet M_v = F·h som forsøker å velte klossen. Men klossen forblir i ro fordi R_y flytter seg mot høyre. Til sammen danner G og R_y et stabiliseringsmoment M_s = G·a som er like stort og motsatt rettet av M_v. a er avstanden mellom G og R_y.

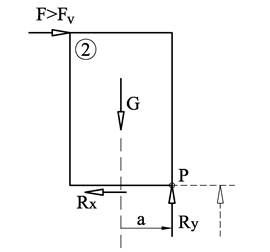
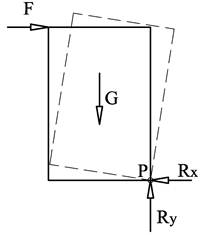
I situasjonen over er den ytre kraft F så stor at klossen velter og dette skyldes at M_v > M_s. Vi får det største stabiliseringsmomentet med R_y i punktet P, men dette momentet er mindre enn veltemomentet. Den stiplede pilen indikerer hvor R_y må angripe for å skape momentlikevekt, men det er selvsagt umulig.

I stedet for å sette opp likevektslikninger ser vi på grensetilfellet hvor legemet er i ferd med å velte. Både R_x og R_y virker i veltepunktet P (dette er jo det eneste kontaktpunktet) og vi setter opp momentuttrykk om P. Vi beregner veltemomentet (M_v =F·h) og sjekker om dette er større enn det stabiliseringsmomentet (M_s =G·b/2). En stabiliseringsoppgave begynner med å bestemme veltepunktet.